Лекция 6

(Закон Брюстера. Закон Малюса. Вращение плоскости поляризации.)

2.3.3 Закон Брюстера

Закон Брюстера позволяет определить угол падения (угол Брюстера), при котором отраженный от поверхности данного диэлектрика луч, полностью поляризован:

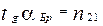(2.11)

Если луч света падает на поверхность диэлектрика под углом Брюстера, то отраженный луч является полностью поляризованным, причем плоскость колебаний вектора Е перпендикулярна плоскости падения, а угол, образованный отраженным и преломленным лучами, составляет . Проведем доказательство этого утверждения. При доказательстве будем исходить из опытного факта существования для каждого диэлектрика определенного угла падения неполяризованного света, при котором отраженный луч полностью поляризован, и его плоскость поляризации совпадает с плоскостью падения (см. рис. 2.22)

Прошедший в диэлектрик луч содержит две компоненты, соответствующих двум взаимно-ортогональным поляризациям. Однако в нем преобладает компонента с плоскостью колебаний, совпадающей с плоскостью падения. На рисунке 2.23 показана только эта компонента падающего и преломленного лучей.

Обозначим амплитуды векторов напряженности в первой и второй средах указанной компоненты электромагнитной волны соответственно и .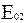

Мы знаем, что при переходе через границу двух диэлектриков нормальная составляющая вектора напряженности электрического поля уменьшается пропорционально отношению диэлектрических проницаемостей, а тангенциальная составляющая остается неизменной, т.е.

(2.12)

(2.13)

Или, учитывая закон преломления (закон Снелиуса):

sin /sin 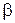= n₂₁ (2.14)

и тот факт, что

,

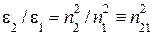получим, поделив соответствующие части (I) и (2):

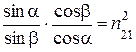
Откуда следует:

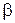cos /cos = n₂₁

и 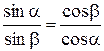. (2.15)

Равенство (2.15) возможно лишь в том случае, когда выполнены равенства:

sin =cos 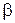(2.16)

sin 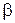=cos (2.17)

Поэтому формулу (2.14) можно переписать в виде:

.

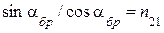Кроме того, равенства (2.16) и (2.17) предполагают существование простой связи между углами и :

.

(Последнее проверить самостоятельно методом подстановки).

2.3.4 Закон Малюса

Закон Малюса гласит: интенсивность света, прошедшего через анализатор, равна интенсивности света, прошедшего через поляризатор, умноженной на квадрат косинуса угла, образованного между поляризатором и анализатором:

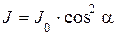(2.18)

В данном случае используются две поляризационные пластинки (см. рис.2.24). Неполяризованный свет падает на первую из них, называемую поляризатором; прошедшая через поляризатор компонента светового пучка поляризована.

Ориентация плоскости колебаний вектора прошедшей волны соответствует ориентации поляризатора. Интенсивность меньше, чем у естественного света:

.

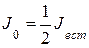Через вторую поляризационную пластинку, называемую анализатором, проходит часть поляризованной волны с поляризацией, параллельной анализатору. Интенсивность снова уменьшается:

(Учитывая, что интенсивность электромагнитной волны пропорциональна квадрату амплитуды напряженности электрического поля, мы приходим к формуле закона Малюса.) При параллельных поляризаторах интенсивность прошедшего света максимальна:

,

при скрещенных – минимальна:

2.3.5 Вращение плоскости поляризации

В прозрачных аморфных телах, а также в кристаллах кубической системы может возникать двойное лучепреломление под влиянием внешних воздействий, например, при механических деформациях тел. Поместим стеклянную пластинку между скрещенными поляризаторами как на верхнем рисунке (рис.2.25). Пока стекло не деформировано, такая система света не пропускает. Если же пластинку подвергнуть сжатию, свет через систему начинает проходить; экран будет испещрен цветными полосами. Каждая такая полоса соответствует одинаково деформированным местам пластинки. Эффект вращения плоскости поляризации в пластинке оказывается различным для различных длин волн. На этом основан оптический метод исследования напряжений.

Возникновение двойного лучепреломления в жидкостях и в аморфных твердых телах под воздействием электрического поля было обнаружено Керром в 1875 г. Это явление получило название эффекта КЕРРА. Схема установки для наблюдения эффекта Керра показана на нижнем рисунке (рис.2.26). Ячейка Керра представляет собой сосуд с жидкостью, в который введены пластины конденсатора. Эффект Керра объясняется различной поляризуемостью молекул по разным направлениям. В отсутствие поля молекулы ориентированны хаотическим образом. Под действием поля молекулы поворачиваются, происходит поляризация жидкости, при этом она становится оптически анизотропной. Ячейка Керра используется как практически безинерционный оптический затвор.

Известно двойное лучепреломление жидких сред, молекулы которых имеют вытянутую форму, под действием ультразвука (акустическое двойное лучепреломление).

Некоторые растворы (например, водный раствор сахара) обладают способностью вызывать вращение плоскости поляризации проходящего через них плоскополяризованного света / оптически активные вещества / Угол поворота плоскости поляризации пропорционален длине пути света в растворе и концентрации активного вещества с: , где - удельная постоянная вращения.

ЭФФЕКТ ФАРАДЕЯ - вращение плоскости поляризации веществом, помещенным в магнитное поле; при этом угол поворота пропорционален напряженности магнитного поля: 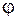~H.

Date: 2015-05-08; view: 865; Нарушение авторских прав