Интерференция когерентных волн

2.1.1. Условия максимума и минимума интерференции когерентных волн

Когерентными называют две волны, у которых одинаковые частоты, и разность фаз не изменяется со временем.

Интерференция света – пространственное перераспределение светового потока при наложении двух (или нескольких) волн, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности.

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга и наблюдается интерференционная картина. Практически это можно осуществить с помощью щелей, зеркал, лазеров и экранов.

Две когерентные волны, приходя в данную точку, вызывают в ней гармонические колебания:

y₁=y₀₁·cos(ωt+φ₁),

y₂=y₀₂·cos(ωt+φ₂)

Если разность фаз указанных колебаний удовлетворяет равенству:

∆φ ≡ φ₂-φ₁=2m·π, (2.1)

(m=0,1,2,…)

то амплитуда результирующего колебания является суммой амплитуд интерферирующих волн (см. рис. 2.1):

y₀=y₀₁+y₀₂

Если же разность фаз составляет нечетное число π, т.е.:

∆φ=(2m+1)·π, (2.2)

то волны ослабляют друг друга; амплитуда результирующего колебания становится равной:

y₀=|y₀₂ - y₀₁|

При равенстве амплитуд интерферирующих колебаний в первом случае имеем:

y₀=2y₀₁=2y₀₂,

а во втором - y₀=0.

Уравнения двух когерентных волн, распространяющихся в двух различных средах с показателями преломления n₁ и n₂, имеют вид:

y₁=y₀₁·cos(ωt-k₁х₁),

y₂=y₀₂·cos(ωt-k₂х₂),

Если в первой среде волна проходит расстояние х=l₁, а во второй - х=l₂, то ∆φ=k₁l₁-k₂l₂=2π(l₁/λ₁-l₂/λ₂).

Т.к. n₁=λ₀/λ₁, а n₂=λ₀/λ₂, где λ₀ – длина волны в вакууме, то условия максимума и минимума интерференции принимают вид:

σ ≡ n₁l₁-n₂l₂=m·(λ₀/2)·2 (2.3)

σ ≡ n₁l₁-n₂l₂=(2m+1)·(λ₀/2) (2.4)

l₁ – геометрическая длина пути 1-ой волны в 1-ой среде,

n₁l₁ – оптическая длина пути 1-ой волны в 1-ой среде,

σ – оптическая разность хода.

Если оптическая разность хода (n₁l₁-n₂l₂) двух интерферирующих волн равна целому числу длин волн в вакууме (или четному числу полуволн), то при интерференции получается максимум колебаний. Если же оптическая разность хода равна нечетному числу полуволн, то при интерференции получается минимум колебаний.

Ошибочно думать, что в точках волнового поля, в которых наблюдается минимум колебаний, происходит бесследное исчезновение энергии волн. В действительности нет нарушения закона сохранения энергии и в данном явлении, т.к. в результате интерференции происходит лишь перераспределение энергии волнового поля.

2.1.2. Интерференция при отражении света от тонких пластинок

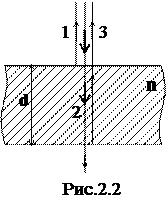Пусть на плоскопараллельную оптически прозрачную пластинку толщиной d падает плоская монохроматическая световая волна (см. рис. 2.2).

На верхней поверхности происходит расщепление светового пучка на отраженный и проведший в пластинку лучи (1 и 2 соответственно). Если пластинку окружает воздух, показатель преломления которого считаем равным 1, то пластинка, у которой n>1, является оптически более плотной средой. При отражении световой волны от оптически более плотной среды наблюдается потеря полуволны. В результате чего оптическая разность хода между волнами, отраженными от нижней- 3 и верхней- 1 поверхности пластинки составляет:

σ₁₃=2n d - (λ₀/2)

Если выполняется равенство σ₁₃ = mλ₀, то пластинка представляется нам в отраженном свете освещенной, если же σ₁₃ = (2m+1)(λ₀/2), тo пластинка не видна. Указанное явление получило важное практическое применение в «просветлении» оптических систем.

При использовании многолинзовых оптических систем (объективы фотоаппаратов, теле- или кинокамер, стереотруб, биноклей и др.) возникает проблема ослабления светового пучка, прошедшего через систему стекол, появления бликов отраженных пучков света. Для устранения такого рода помех поверхности линз покрывают тонким слоем светопрозрачного вещества (см. рис. 2.3).

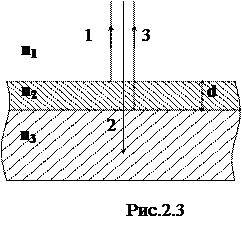При этом толщину слоя подбирают такой, чтобы отраженные лучи 1 и 3 гасили друг друга. Вещество слоя имеет промежуточный показатель преломления, т.е. n₁<n₂<n₃, поэтому оба луча 1 и 3 отражаются с потерей полуволны. В результате оптическая разность хода составляет:

σ = 2n₂d.

Поставленная цель достигается, если:

σ = λ₀/2,

2n₂ d =λ₀/2.

Откуда: d = λ₀/(4·n₂) = λ_в/4.

Длина волны зеленого света (наиболее благоприятного для восприятия человеческим глазом) составляет 0,55мкм. Следовательно, толщина пленки составляет десятые доли микрометра. (Объяснить самостоятельно - почему просветленная оптика в отраженном свете представляется нам окрашенной в сиреневый цвет).

2.1.3. Интерференция в тонком клине

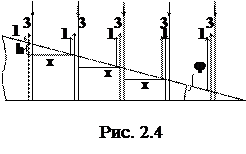Представим себе, что плоская световая монохроматическая волна падает на тонкий клин, изготовленный из оптически прозрачного вещества, перпендикулярно к его основанию (см. рис. 2.4).

Клин настолько тонок, что отраженные лучи 1 и 3 идут практически параллельно друг другу вертикально вверх. Рассматриваемый сверху в отраженном свете клин представится нам «полосатым», причем световые полосы, чередуемые с темными полосами, будут параллельны острой кромке клина и будут находиться на равном расстоянии друг от друга - х.

Для двух соседних максимумов интерференции (двух соседних полос) можем записать:

2nd - (λ₀/2) = mλ₀

2n(d+h) - (λ₀/2) = (m+1)λ₀

Вычитая из одного равенства другое, получим:

2nh = λ₀

Т.к. h = х·tgφ ≈ х·φ,

то 2nхφ = λ₀.

Откуда следует:

х = λ₀/2nφ,

следовательно, расстояние между соседними светлыми (темными) полосами тем больше, чем тоньше клин. В пределе при φ → 0 поверхность клина представляется нам либо равномерно освещенной, либо равномерно затемненной.

Явление интерференции в оптически прозрачном клине нашло очень важное применение в технологии изготовления оптических линз. Ведь линза представляет своеобразный клин (хотя его поверхности не являются плоскими). Наблюдая за поверхностью линзы в отраженном свете можно по искривлению интерференционных полос обнаружить очень незначительные дефекты - неровности поверхности, неоднородность стекла.

2.1.4. Интерферометр Майкельсона

Рекордная точность в измерениях длины линейных отрезков (перемещений) достигается с помощью интерферометра Майкельсона, схема которого изображена на рис. 2.5.

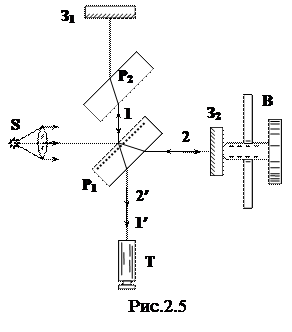Пучок света от источника S падает на полупрозрачную пластинку P₁, покрытую тонким слоем серебра. Половина упавшего светового потока отражается пластиной Р₁ в направлении луча 1, половина проходит сквозь пластинку и распространяется в направлении луча 2. Пучок 1 отражается от зеркала З₁, и возвращается к P₁. Пучок 2, отразившись от зеркала З₂, тоже возвращается к пластине Р₁. Прошедшие через пластинку Р₁ лучи 1^/ и 2^/ когерентны между собой и имеют одинаковую интенсивность. Результат интерференции этих пучков зависит от оптической разности хода от пластинки Р₁ до зеркал 3₁ и З₂ и обратно. Луч 2 проходит толщину пластинки трижды, луч 1 - только 1 раз. Чтобы скомпенсировать возникающую за счет этого разную (вследствие дисперсии) для различных длин волн и различных температур оптическую разность хода, на пути луча 1 ставится точно такая, как Р₁, но не посеребренная пластинка Р₂.Тем самым уравниваются пути лучей 1 и 2 в стекле. Интерференционная картина наблюдается с помощью зрительной трубы Т. Вращая микрометрический винт В, можно плавно перемещать зеркало 3₂, тем самым можно изменять оптическую разность хода между лучами 1^/ и 2^/.

2n·∆L=2·N·λ₀/2 (max), где n = 1.

Пусть в результате вращения микрометрического винта зеркало З₂ переместилось вдоль измеряемого отрезка на ∆L, при этом наблюдая в зрительную трубу, мы зафиксировали N интерференционных миганий. Нетрудно получить ∆L=N·λ₀/2. Откуда следует, что цена деления измерительного прибора составляет λ₀/2, т.е. для зеленого света она равна 0,27 мкм.

2.1.5. Интерференционные рефрактометры

Позволяют определить незначительные изменения показателя преломления прозрачных тел в зависимости от давления, температуры и т.д.

На пути интерферирующих лучей помещаются две одинаковые кюветы длиной l. Одна заполнена газом с известным показателем преломления n₀, а другая – с неизвестным – n_х.Возникает дополнительная разность хода δ = (n_х – n₀)∙ l, которая приводит к сдвигу интерференционных полос. Величина показывает, на какую часть ширины интерференционной полосы сместилась интерференционная картина. (Т.к. δ = (n_х· l – n₀∙ l) = m λ)

Измеряя m₀ (при известных l, n₀, λ), можно найти n_х.

Date: 2015-05-08; view: 2846; Нарушение авторских прав