Дифракция света. 2.2.1. Принцип Гюйгенса-Френеля

2.2.1. Принцип Гюйгенса-Френеля

Дифракцией называют явление огибания световыми волнами препятствий и проникновения света в область геометрической тени. Дифракция представляет собой частный случай интерференции, когда перераспределение интенсивности, происходит вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно. (При «обычной» интерференции рассматривается, как правило, два когерентных источника).

Различают два вида дифракции: дифракция Фраунгофера (дифракция в параллельных лучах) и дифракция Френеля (дифракция в сходящихся лучах). Проникновение световых волн в область тени может быть объяснено с помощью принципа Гюйгенса-Френеля (Г-Ф). Согласно принципу Г-Ф каждый элемент волновой поверхности (см. рис.2.6) служит источником вторичной волны, амплитуда которой пропорциональна величине элемента dS, убывает с расстоянием r от источника по закону 1/r:

dА = К₀(А₀·dS)/r ·cos(ωt+φ₀-kr) (2.5)

где А₀ - амплитуда колебаний на поверхности S,

К₀ - коэффициент, зависящий от ориентации площадки dS, т.e. от угла α. (Если α=0, то К₀=1, если α→π/2, то К₀→0), (ωt+φ₀) - фаза колебания в месте расположения волновой поверхности S, k - волновое число, Р - точка наблюдения.

Результирующее колебание представляет собой cyперпозицию элементарных колебаний.

А= 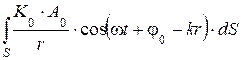(2.6)

Эта формула является аналитическим представлением принципа.

2.2.2 Зоны Френеля

Вычисление по формуле (2.6) представляет собой в общем случае трудную задачу. Однако, как показал Френель, в случаях, отличающихся симметрией, нахождение амплитуды результирующего колебания может быть осуществлено простым алгебраическим суммированием.

Определим амплитуду светового колебания, возбуждаемого в точке Р сферической волной, распространяющейся в изотропной однородной среде из точечного источника S (рис. 2.7). Волновые поверхности симметричны относительно прямой 0Р.

Разобьем выбранную волновую поверхность на кольцевые зоны, разность хода от границ которых до точки Р составляет λ/2. Это зоны Френеля.

r₁ = r₀+λ/2; r₂ = r₁+λ/2 = r₀+2λ/2;

r₃ = r₂+λ/2 = r₀+3λ/2; r₄ = r₀+4λ/2…

Волны, приходящие в Р от точек каждой последующей зоны, сдвинуты по отношению к волнам, приходящим от соответствующих точек предыдущей зовы, на λ/2, т.е. находятся в противофазах и их амплитуды вычитаются. Обозначим амплитуду волн, приходящих в Р от каждой последующей зоны, так: А₀, А₁, А₂, А₃, А₄,…… Величины этих амплитуд монотонно убывают, т.к. возрастает расстояние r и увеличивается угол α (т.е. убывает коэффициент К₀). Следовательно: А₀>А₁>А₂>А₃>А₄… Естественно считать, что выполняется система равенств:

А₁ = 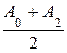, А₂ = 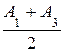, А₃ = ,…

Тогда, учитывая противофазность волн, приходящих от соседних зон, получим:

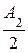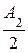А = А₀ - А₁ + А₂ - А₃ + А₄ - А₅ +……= + ( -А₁+ ) + ( -А₃+ ) +….≡ .

Таким образом, суммарная амплитуда от воздействия всего фронта в точке Р равна , т.е. эквивалентна половине воздействия нулевой зоны Ф.

Если поставить экран, пропускающий лучи только от нулевой зоны, то амплитуда колебания увеличиться в 2, а интенсивность света - в 4 раза!!!

Эффект можно еще усилить, если поставить на пути света зонную пластинку, пропускающую свет только от четных (или только от нечетных) зон Френеля.

Тогда:

А = А₀+А₂+А₄+А₆+А₈+……

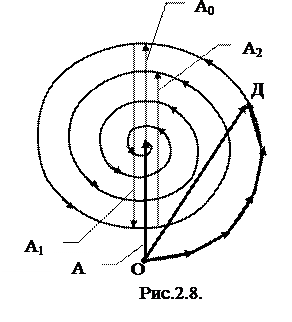Очень наглядной оказывается векторная диаграмма сложения колебаний (рис.2.8).

Каждой элементарной кольцевой зоне соответствует элементарный вектор, угол наклона которого равен отставанию по фазе колебания, пришедшего из данной кольцевой зоны, от колебания, приведшего из точки 0. В результате сложения векторов от всех элементов волновой поверхности получается кривая, представляющая собой спираль. Если взять на этой спирали т. Д, то она соответствует фрагменту нулевой зоны с разностью хода λ/4. От внутренней половины нулевой зоны приходит волна с амплитудой . (Самостоятельно показать на векторной диаграмме вектора, соответствующие колебаниям от нулевой, первой и второй зон Френеля).

2.2.3 Дифракция Фраунгофера от щели.

Пусть на плоскопараллельную щель падает плоская монохроматическая волна. Поместим за щелью собирающую линзу, а в фокальной плоскости линзы - экран (см. рис.2.9). Когда световая волна достигает отверстия щели, то каждая точка согласно принципу Гюйгенса становится источником сферических волн, распространяющихся по всем направлениям.

Из этого множества лучей выберем лучи, идущие под углом φ к волновому вектору. Пусть 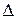составляет целое число , например, т.е. рассматриваемая в выбранном направлении волновая поверхность ОА состоит из 3-х зон Френеля. Если Z - число зон Ф., то Z .

При Z = 2m получим минимум интерференции, а при Z = 2m+1 - максимум интерференции, следовательно, условие максимума для дифракции от щели:

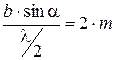
или . (2.7)

(Для вакуума )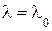

Условие минимума: (2.8)

Date: 2015-05-08; view: 733; Нарушение авторских прав