Прямая перпендикулярна плоскости

В данном параграфе мы разберём ещё несколько распространённых задач. Чувствую, вы немного заскучали, поэтому пора предложить живительные примеры для самостоятельного решения. А потом ещё десяток =)

Пример 4

Дана плоскость 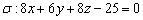и точка 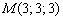. Требуется:

а) составить канонические уравнения прямой 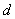, проходящей через точку 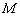, перпендикулярно данной плоскости;

б) найти точку 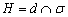пересечения перпендикулярной прямой и плоскости;

в) найти точку 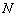, симметричную точке 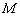относительно плоскости .

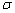Идейно похожая «плоская» задача рассмотрена на уроке Задачи с прямой на плоскости.

Выполним схематический чертёж и коротко разберём алгоритм решения:

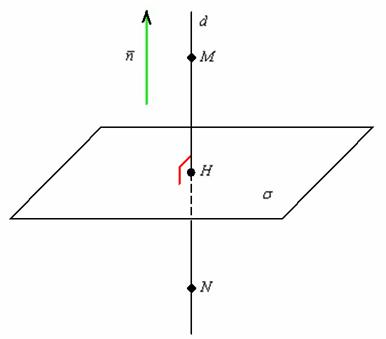
а) Как составить уравнения перпендикулярной прямой «дэ», думаю, объяснять не нужно. Подсказка есть прямо на чертеже.

б) Точка пересечения перпендикулярной прямой и плоскости находится обычным способом (см. п. «б» предыдущего примера). К слову, точка является проекцией прямой на плоскость «сигма».

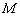в) Рассмотрим отрезок . Если точка симметрична точке относительно плоскости, то, очевидно 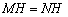. Саму длину перпендикуляра 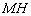мы рассчитывали в Примере №9 на уроке Уравнение плоскости, но сейчас речь не о длине. Точка делит отрезок пополам. По условию нам дан один из концов отрезка 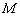, а в предыдущем пункте найдена середина . Таким образом, по формулам деления отрезка пополам, нетрудно найти координаты нужной точки .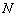

Полное решение и ответ в конце урока. Постарайтесь не заглядывать в образец, сложного-то здесь ничего нет.

Вопрос очевидный, но на всякий случай коснёмся обратной задачи: как составить уравнение плоскости, которая проходит через данную точку перпендикулярно данной прямой? Берём направляющий вектор прямой – он же является вектором нормали плоскости.

Поставлю и другую заплату, вроде в явном виде нигде не упоминал: можно ли составить уравнение плоскости, проходящей через прямую и точку, не принадлежащую прямой? Да, конечно, причём плоскость будет определена однозначно. Конкретный пример можно посмотреть в Пункте №12 задачи с треугольной пирамидой.

Все задачи на пересечение прямой и плоскости, пожалуй, исчерпаны, теперь рассмотрим что-нибудь на прямую, параллельную плоскости. Таких примеров я отыскал совсем немного, и решил приютить одного сироту:

Пример 5

Даны скрещивающиеся прямые 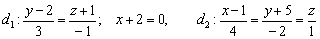. Через прямую 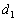провести плоскость, параллельную прямой .

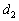Решение: Задача простая, но всё равно выполним схематический чертёж:

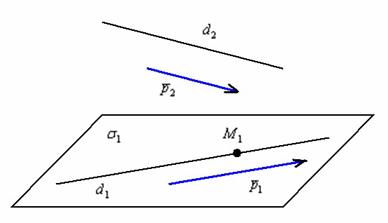
По условию требуется найти уравнение плоскости , которая проходит через прямую параллельно второй прямой.

Уравнение плоскости составим по точке и двум неколлинеарным векторам.

Поскольку прямая должна лежать в плоскости 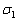, то нам подойдёт произвольная точка 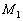, принадлежащая первой прямой, и её направляющий вектор:

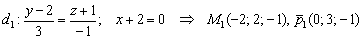
С другой стороны, плоскость 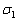должна быть параллельна прямой 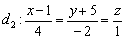, а, значит, и её направляющему вектору .

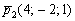Так как прямые скрещиваются, то их направляющие векторы 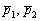будут не коллинеарны.

Уравнение плоскости 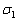составим по точке 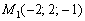и двум неколлинеарным векторам :

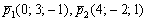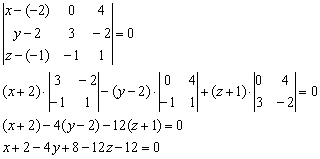
Ответ: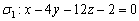

Используя материалы начала урока, можно выполнить проверку – убедиться, что первая прямая действительно лежит в полученной плоскости, а вторая прямая – параллельна ей.

Аналогично можно составить уравнение плоскости 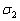, которая проходит через прямую 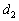параллельно прямой 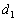. Решение будет точно таким же, изменится только точка – необходимо взять какую-нибудь точку, принадлежащую второй прямой. Очевидно, что данные плоскости будут параллельны: .

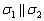Другие задачи по пространственной геометрии можно закачать на странице Бесплатные решения задач по высшей математике, только что заново пересмотрел свой архив, несколько десятков примеров точно есть.

По ходу создания данного урока мне совершенно случайно попалась на глаза одна методичка для студентов-заочников, где среди прочих заданий, как раз есть десять задач по аналитической геометрии в пространстве. Находка оказалась очень своевременной и удачной, поскольку предоставила отличную возможность дополнительно наполнить эту статью полезным материалом, а также прикинуть, насколько пОлно я рассмотрел всю тему. То есть, провести ещё и небольшое самотестирование.

Добро пожаловать в «реальные боевые условия»:

Я перепишу условия всех 10-ти задач и кратко прокомментирую, как их решать. Желающие могут частично или полностью выполнить данные задания, правильные ответы – в конце урока.

1) Из точки 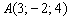опустить перпендикуляр на плоскость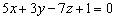

Смотрите Пример №4 данного урока, пункт «а».

2) Найти проекцию точки 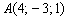на плоскость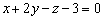

Проекция точки на плоскость – это в точности основание перпендикуляра, смотрите Пример №4 данного урока, пункт «б».

3) Через прямую 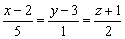провести плоскость, перпендикулярную к плоскости .

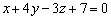Смотрите Пример №3 данного урока, пункт «в».

4) Написать уравнение плоскости, проходящей через две параллельные прямые 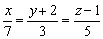и

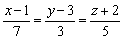
Смотрите Пример №17 урока Задачи с прямой в пространстве, пункт «б».

5) Составить уравнение плоскости, проходящей через точку 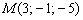перпендикулярно плоскостям 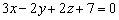и .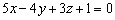

Вот этой задачи нигде не встречалось. Уравнение искомой плоскости нужно составить по точке 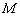и двум нормальным векторам плоскостей.

6) Найти длину перпендикуляра, опущенного из точки 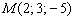на плоскость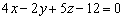

Смотрите Пример №9 урока Уравнение плоскости.

7) Найти уравнение плоскости, зная, что точка 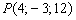служит основанием перпендикуляра, опущенного из начала координат на эту плоскость.

Фактически нужно составить уравнение плоскости по точке 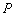и вектору нормали 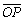, где точка 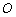– начало координат.

8) Найти расстояние от точки 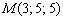до прямой .

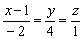Смотрите Пример №15 урока Задачи с прямой в пространстве, пункт «б».

9) Через начало координат провести плоскость, перпендикулярную прямой .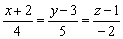

Необходимо составить уравнение плоскости по точке и вектору нормали.

10) Найти уравнения перпендикуляра, опущенного из точки 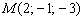на прямую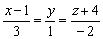

Смотрите Пример №15 урока Задачи с прямой в пространстве, пункт «а».

Ну что же, из 10-ти пробных задач не разобрана только одна (№5), да и та простая. Таким образом, примерно с 90%-ой вероятностью, вы должны найти то, что нужно. Иногда, конечно, встречаются трудные задачи или задачи с дОнельзя зашифрованным условием, но это редкость.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: Найдем направляющий вектор и точку, принадлежащую прямой:

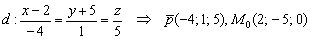
Найдём вектор нормали плоскости:
.
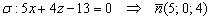Вычислим скалярное произведение:
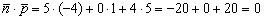, значит, прямая параллельна плоскости или лежит в ней.
Подставим координаты точки 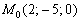в уравнение плоскости :

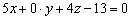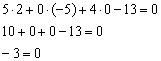
Получено неверное равенство, значит, точка 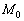не лежит в плоскости 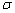, и все точки прямой не лежат в данной плоскости.
Ответ: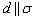

Пример 4: Решение:
а) Найдём вектор нормали плоскости: 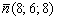. Уравнения перпендикулярной прямой составим по точке 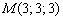и вектору нормали :

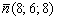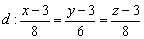
б) Перепишем уравнения прямой в параметрической форме:

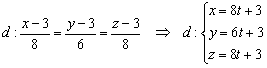
Основание перпендикуляра принадлежит данной прямой, и координатам данной точки соответствует определённое значение параметра: 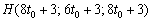. Но точка также принадлежит и плоскости. Подставим параметрические координаты в уравнение плоскости:

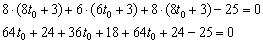
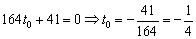– подставим найденное значение параметра в параметрические координаты точки:

в) Координаты симметричной точки 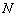найдем по формулам координат середины отрезка:

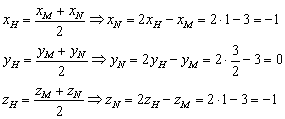
Таким образом: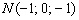
Ответ:
а) ;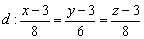
б) ;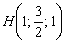
в) .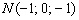

Ответы на 10 задач:

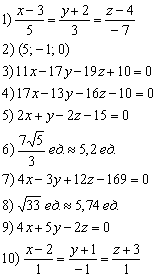
Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Date: 2015-04-23; view: 1251; Нарушение авторских прав