Как найти угол между прямой и плоскостью?

д) Логическое продолжение темы.

Если прямая 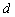не перпендикулярна плоскости 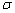, то углом 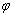между прямой и плоскостью называется острый угол между прямой 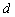и её проекцией на плоскость 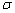. Если прямая перпендикулярна плоскости, то угол между ними равен 90 градусов.

Продолжим эксплуатацию геометрического инвентаря:

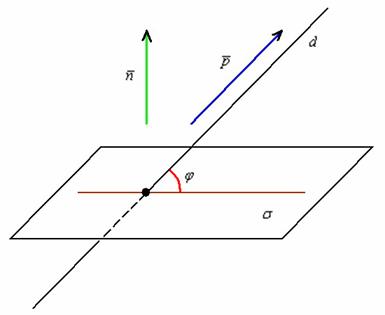
Справедлива следующая формула синуса угла между прямой и плоскостью:

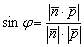
Таким образом, для нахождения данной угла достаточно знать лишь нормальный вектор плоскости и направляющий вектор прямой. При необходимости вывод формулы можно посмотреть, например, в учебнике Атанасяна-Базылева. А мы займёмся практическим решением.

Скалярное произведение векторов уже найдено в пункте «а»: 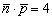. Обратите внимание, что в формуле скалярное произведение находится под знаком модуля, который «съедает» возможный «минус».

Вычислим длины векторов:

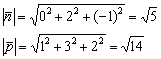
По формуле: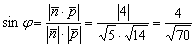

На иррациональность в знаменателе забиваем, поскольку нам нужен сам угол:

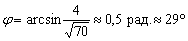
Выложим в ряд головы очередного Змея-Горыныча:

Ответ:
а) 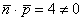, значит, прямая пересекает плоскость;
б) ;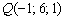
в) ;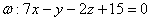
г) ;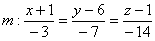
д)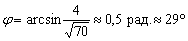

Переходим к рассмотрению частного случая – когда:

Date: 2015-04-23; view: 802; Нарушение авторских прав