Как построить прямую пространства, перпендикулярную данной?

(прямые пересекаются)

Пример 15

а) Составить уравнения прямой, проходящей через точку 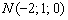перпендикулярно прямой 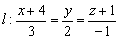(прямые пересекаются).

б) Найти расстояние от точки 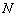до прямой .

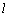Примечание: оговорка «прямые пересекаются» – существенна. Через точку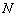
можно провести бесконечно много перпендикулярных прямых, которые будут скрещиваться с прямой «эль». Единственное решение имеет место в случае, когда через данную точку проводится прямая, перпендикулярная двум заданным прямым (см. Пример №13, пункт «б»).

а) Решение: Неизвестную прямую обозначим через 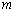. Выполним схематический чертёж:

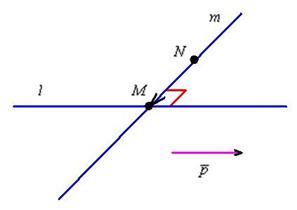
Что известно о прямой 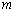? По условию дана точка 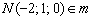. Для того, чтобы составить уравнения прямой, необходимо найти направляющий вектор. В качестве такого вектора вполне подойдёт вектор 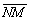, им и займемся. Точнее, возьмём за шкирку неизвестный конец вектора.

1) Вытащим из уравнений прямой «эль» её направляющий вектор , а сами уравнения перепишем в параметрической форме:

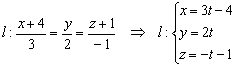
Многие догадались, сейчас уже в третий раз за урок фокусник достанет белого лебедя из шляпы. Рассмотрим точку 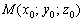с неизвестными координатами. Поскольку точка 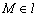, то её координаты 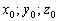удовлетворяют параметрическим уравнениям прямой «эль» и им соответствует конкретное значение параметра:

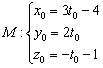
Или одной строкой: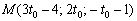

Тогда: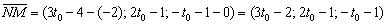

2) По условию прямые должны быть перпендикулярны, следовательно, их направляющие векторы 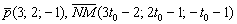– ортогональны. А если векторы ортогональны, то их скалярное произведение равно нулю:

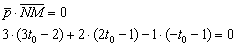
Что получилось? Простейшее линейное уравнение с одной неизвестной:

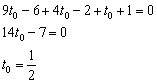
3) Значение параметра известно, найдём точку:

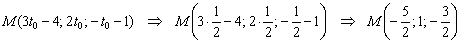
И направляющий вектор:
.

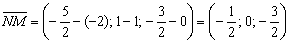4) Уравнения прямой 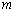составим по точке 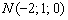и направляющему вектору :

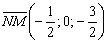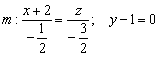
Знаменатели пропорции получились дробные, и это как раз тот случай, когда от дробей уместно избавиться. Я просто умножу их на –2:

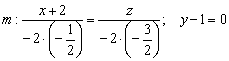
Ответ: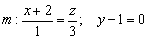

Примечание: более строгая концовка решения оформляется так: составим уравнения прямой по точке 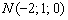и направляющему вектору 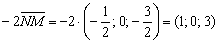. Действительно, если вектор 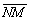является навправляющим вектором прямой, то коллинеарный ему вектор 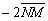, естественно, тоже будет направляющим вектором данной прямой.

Проверка состоит из двух этапов:

1) проверяем направляющие векторы прямых на ортогональность;

2) подставляем координаты точки 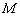в уравнения каждой прямой, они должны «подходить» и там и там.

О типовых действиях говорилось очень много, поэтому я выполнил проверку на черновике.

Кстати, запамятовал ещё пунктик – построить точку «зю» симметричную точке «эн» относительно прямой «эль». Впрочем, есть хороший «плоский аналог», с которым можно ознакомиться в статье Простейшие задачи с прямой на плоскости. Здесь же всё отличие будет в дополнительной «зетовой» координате.

Date: 2015-04-23; view: 885; Нарушение авторских прав