Как выяснить взаимное расположение прямой и плоскости?

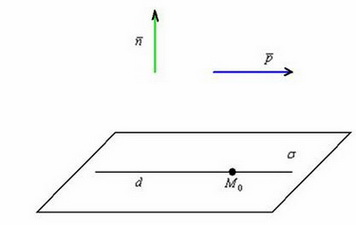
Изучим аналитические условия, которые позволят нам ответить на данный вопрос. Выполним схематический чертёж, на котором прямая пересекает плоскость:

Прямая пересекает плоскость тогда и только тогда, когда её направляющий вектор не ортогонален вектору нормали 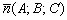плоскости.

Из утверждения следует, что скалярное произведение вектора нормали и направляющего вектора будет отлично от нуля: .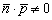

В координатах условие запишется следующим образом:

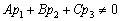
Если же данные векторы ортогональны, то есть если их скалярное произведение равно нулю: , то прямая либо параллельна плоскости, либо лежит в ней:

Разграничим данные случаи.

Если прямая параллельна плоскости, то точка 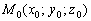(а, значит, и ЛЮБАЯ точка данной прямой) не удовлетворяет уравнению плоскости: .

Таким образом, условие параллельности прямой и плоскости записывается следующей системой:

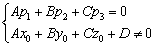
Если прямая лежит в плоскости, то точка (а, значит, и ЛЮБАЯ точка данной прямой) удовлетворяет уравнению плоскости: .

Аналитические условия данного случая запишутся похожей системой:

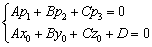
Разборки с взаимным расположением прямой и плоскости достаточно примитивны – всего в два шага. Кроме того, на практике можно обойтись даже без всяких систем. Исследование взаимного расположения прямых в пространстве, которое проводилось на уроке Задачи с прямой в пространстве, намного трудозатратнее. А тут всё проще:

Пример 1

Выяснить взаимное расположение прямой, заданной точкой 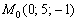и направляющим вектором , и плоскости .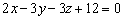

Решение: Вытащим вектор нормали плоскости: .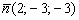

Вычислим скалярное произведение вектора нормали плоскости и направляющего вектора прямой: 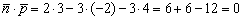, значит, прямая либо параллельна плоскости, либо лежит в ней.

Подставим координаты точки 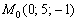в уравнение плоскости:

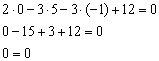
Получено верное равенство, следовательно, точка лежит в данной плоскости. Разумеется, и любая точка прямой тоже будет принадлежать плоскости.

Ответ: прямая лежит в плоскости

Пример 2

Выяснить взаимное расположение плоскости 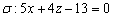и прямой .

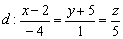Это пример для самостоятельного решения. Примерный образец оформления и ответ в конце урока.

После небольшой разминки мускулатуры начинаем накидывать блины на штангу:

Date: 2015-04-23; view: 1012; Нарушение авторских прав