Как найти точку пересечения прямой и плоскости?

б) Найдём точку пересечения плоскости и прямой: 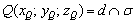. Не «Чёрный квадрат» Малевича, но тоже шедевр:

Приём решения стандартен и хорошо известен из статьи Задачи с прямой в пространстве. Сначала перепишем уравнения прямой в параметрической форме:

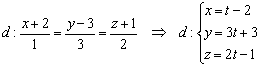
Точка 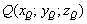принадлежит данной прямой, поэтому её координаты 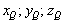при некотором значении параметра 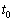удовлетворяют параметрическим уравнениям:
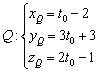, или одной строчкой: .

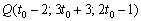С другой стороны, точка 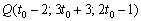принадлежит и плоскости 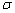, следовательно, координаты точки должны удовлетворять уравнению плоскости 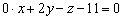, то есть должно выполняться равенство:

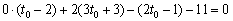– ну, или попросту параметрические координаты точки нужно подставить в уравнение плоскости.

Раскрываем скобки, приводим подобные слагаемые и находим «тэ нулевое»:

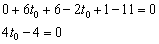
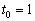– полученное значение параметра подставляем в параметрические выражения координат нашей точки:

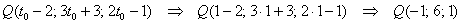
Интересно, что в данном пункте всё обошлось даже без векторов.

Чистка хвоста очевидна: координаты точки 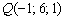должны «подходить» и в уравнения прямой и в уравнение плоскости. Проверку несложно выполнить устно.

в) Найдём уравнение плоскости 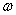, которая перпендикулярна плоскости 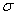и проходит через прямую 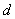. Задача весьма напоминает Пример №12 урока Уравнение плоскости, в котором мы рассмотрели построение перпендикулярной плоскости, проходящей через две точки.

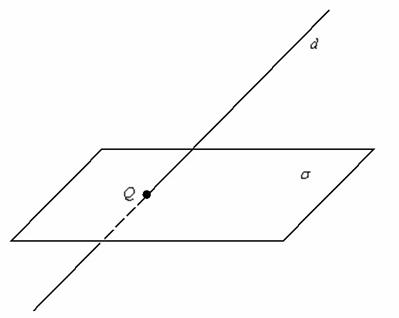
Выполним схематический чертёж:

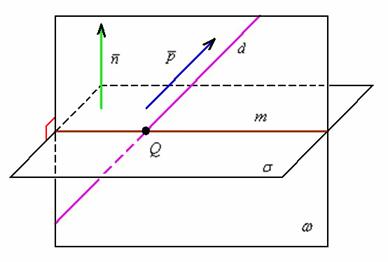
Уравнение плоскости 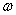можно составить по любой точке, которая принадлежит прямой 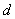, направляющему вектору 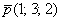прямой 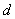и вектору нормали 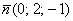плоскости .

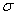В качестве точки, принадлежащей прямой «дэ», не возбраняется, конечно, взять найденную в предыдущем пункте точку пересечения 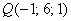, но в произвольной практической задаче она чаще всего не известна. Поэтому обычно используют самую «лёгкую добычу». В данном случае, очевидно, точку:
.

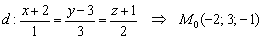Уравнение плоскости «омега» составим по точке 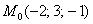и двум неколлинеарным векторам :

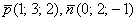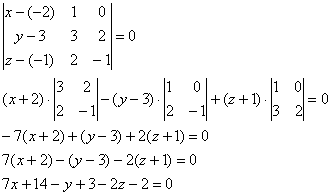
Таким образом: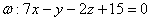

Проверка опять же довольно простая. Устно находим скалярное произведение нормальных векторов 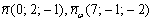двух плоскостей. Оно равно нулю, значит, плоскости перпендикулярны. На втором шаге необходимо убедиться, что прямая «дэ» действительно лежит в найденной плоскости «омега». Можно использовать типовой алгоритм, рассмотренный в самом начале урока. Но тут есть другая возможность – устно подставляем координаты двух известных точек 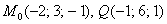в полученное уравнение плоскости 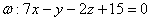. Обе точки «подходят», и это гарантирует, что и вся прямая 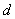лежит в плоскости .

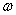Date: 2015-04-23; view: 935; Нарушение авторских прав