Как привести уравнение линии 2-го порядка к каноническому виду?

Задача приведения уравнения линии 2-го порядка к каноническому виду следовала за нами практически с самого начала изучения темы и сейчас мы окончательно разберёмся, как общее уравнение линии второго порядка 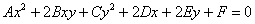(здесь и далее подразумевается, что 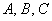не равны одновременно нулю) свести к одному из девяти канонических случаев.

В статьях об эллипсе, гиперболе и параболе, а также на практикуме Задачи с линиями второго порядка очень подробно отработан частный случай уравнения, когда коэффициент :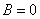

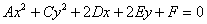
Пожалуйста, внимательно посмотрите на своё уравнение, которое вам нужно привести к каноническому виду – есть ли в нём слагаемое, которое содержит произведение ?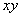

Если такого слагаемого нет, то вам хватит материалов перечисленных выше уроков.

Если же такое слагаемое есть – то не хватит =)

Как многие подметили, члены 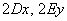общего уравнения «отвечают» за параллельный перенос линии, который имеет место, когда хотя бы один из коэффициентов 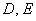отличен от нуля. И логично предположить, что ненулевое слагаемое 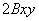«отвечает» за поворот линии. Исключение составляет угол в 90 градусов (а также любой кратный ему угол, например 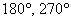), при повороте на который мы отделываемся лёгким испугом, укладываясь в рамки хорошо отшлифованного частного случая 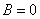. Простейший пример поворота на «нехороший» угол нам уже встречался – это неканонически расположенная «школьная» гипербола 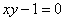(см. Пример 5 статьи Гипербола и парабола).

Уравнение 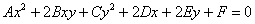с ненулевым коэффициентом «бэ» неприятно тем, что в общем случае его невозможно привести к каноническому виду с помощью обычных средств алгебры: переноса слагаемых, их группировки, вынесений за скобки, выделения полных квадратов и прочей школьной самодеятельности. Поэтому на помощь приходится привлекать более мощные методы решения.

Рассмотрим в качестве примера уравнение 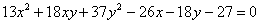. Какие будут идеи? …Да ладно с ними, с идеями, тут даже не понятно, какую линию оно задаёт. Эллипс? Гиперболу? Параболу? Что-то другое из классификации?

Немного потраченного времени, и вы научитесь довольно легко находить ответы на эти вопросы, в частности, без особых проблем сможете определить, что данное уравнение определяет эллипс с полуосями 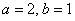, который расположен центром в точке 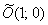и повёрнут относительного своего канонического положения на отрицательный угол, составляющий примерно :

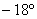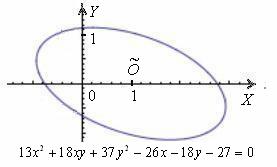
Мысленно возьмите эллипс в руки, поверните его на любой угол и переместите в произвольное место плоскости. Новому положению эллипса будет соответствовать совершенно другое уравнение, и если вам предъявить его без чертежа, то никто в жизнь не догадается, что оно определяет тот же самый эллипс. Именно поэтому и появилась задача приведения уравнения к каноническому виду – чтобы независимо от расположения линии выяснить, что это за зверь и каким нравом он обладает.

На предыдущих уроках я рассматривал два способа приведения. Применительно к нашему примеру:

1) Повернём эллипс на 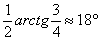(против часовой стрелки) вокруг точки 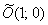и осуществим его параллельный перенос центром в начало координат. В результате получится нужное уравнение .

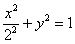2) Перейдём к прямоугольной системе координат 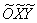, которая получается путём поворота исходной системы координат 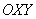на 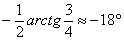вокруг начала координат и её параллельного переноса центром в точку 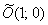. Таким образом, в новой системе координат 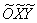уравнение данного эллипса запишется в каноническом виде: .

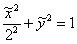Прошу прощения за невысокое качество и точность чертежей данной статьи:

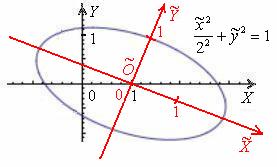
Навскидку второй способ кажется вычурным и неуклюжим, однако, если немного призадуматься, то он более корректен. И толстый намёк на это уже проскочил чуть выше: куда бы мы ни переместили данную линию, какую бы систему координат ни выбрали – эллипс останется тем же самым эллипсом с полуосями 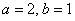, своими фокусами и другими индивидуальными характеристиками.

У многих читателей в пределах досягаемости находится учебник по высшей математике. Пусть это будет его каноническое положение в исходной системе координат. Книгу можно положить на стол, на стул, на кровать, под кровать, в мусорное ведро – да куда угодно. Но учебник останется при этом тем же самым учебником.

То есть, с позиций математики координатная сетка относительна и вторична по отношению к тому или иному объекту. Следовательно, вполне логично и правомерно тревожить именно систему координат, а не «уникальный» эллипс, учебник или что-то ещё. Конечно, с точки зрения физики положение тела имеет большое значение,… …пожалуй, сверну комментарий, а то сейчас набегут любители философии и устроят дискуссию =)

Суть преамбулы состоит в том, что на данном уроке мы будем приводить уравнение линии 2-го порядка путём перехода к новой прямоугольной системе координат, в которой уравнение исследуемой линии примет канонический вид.

Существует несколько практических методов приведения уравнения линии к каноническому виду, причём, некоторые из них являются достаточно трудными. Я постараюсь составить максимально простой конспект, доступный человеку с любым уровнем подготовки.

Все линии 2-го порядка можно разделить на две большие группы:

1) центральные линии, обладающие единственным центром (точкой) симметрии (эллипс, мнимый эллипс, гипербола, пара мнимых или действительных пересекающихся прямых);

2) нецентральные линии, у которых центры симметрии отсутствуют (парабола) либо их бесконечно много (пара действительных или мнимых параллельных прямых, пара совпавших прямых).

Итак, вы счастливый обладатель общего уравнения 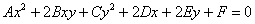с ненулевым коэффициентом 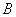. С чего начать? На первом шаге целесообразно выяснить, к какой группе относится линия. Для этого нужно мысленно либо на черновике составить и вычислить определитель 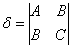. Если 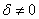, то перед нами уравнение центральной линии, если же 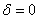– то нецентральной.

Для уравнения :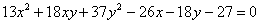
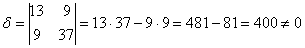, значит, оно определяет центральную линию.

Зачем это нужно? Чтобы подобрать наиболее выгодный способ решения. Конечно, если ваш преподаватель требует строго придерживаться определённого шаблона, то ничего не поделать…. Тем не менее, я постараюсь провести вас самой комфортной и короткой тропинкой через дебри.

Для приведения уравнения центральной линии, по моему мнению, лучше всего использовать метод инвариантов. Но, к сожалению, он перестаёт работать в нецентральном случае, поэтому на помощь придётся привлечь достаточно трудоёмкий универсальный способ решения. Сначала разберём одно, затем другое, и даже если вам нужно разобраться только с нецентральной линией, постарайтесь не пропускать первый параграф, поскольку вся информация взаимосвязана:

Приведение уравнения центральной линии. Метод инвариантов

Во-первых, разберёмся с термином. Инвариант – это величина, которая остаётся неизменной при тех или иных преобразованиях.

Простейший пример геометрического инварианта – это длина отрезка относительно его параллельного переноса. В результате данного преобразовании меняются координаты концов отрезка, но его длина остаётся неизменной (инвариантной).

В частности, длина и ширина учебника по высшей математике (который можно положить на стол, на стул, на кровать, под кровать, в мусорное ведро) – это инварианты относительно перемещения книги в пространстве. А вот если ненавистный томик… чего студент боится больше всего? …матана порвать в клочья, то его размеры уже перестанут быть инвариантами относительно этих механических повреждений =) Но инвариантом останется сам математический анализ. Так что рви, не рви, а осваивать его придётся =)

Однако вернёмся к нашему демонстрационному уравнению 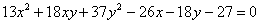. Очевидно, что можно выбрать бесконечно много других прямоугольных систем координат и получить бесконечно много разных уравнений вида 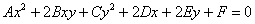, которые задают один и тот же эллипс. И возникает вопрос: а есть ли у этого множества уравнений что-то одинаковое, характерное только для данной линии? Иными словами, есть ли инварианты?

Да, есть! Если уравнение линии 2-го порядка задано общим видом 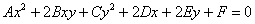в некоторой прямоугольной системе координат, то инвариантами относительно поворота и параллельного переноса прямоугольной системы координат являются следующие ЧИСЛА:

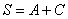– сумма коэффициентов при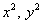

старый знакомец:

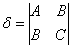
и ещё один определитель:

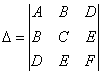
Рассмотрим общее уравнение линии 2-го порядка 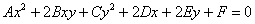и поставим задачу подобрать новую прямоугольную систему координат 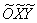ТАК, чтобы уравнение данной линии приняло вид 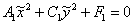(который элементарно сводится к канонической форме). Заметим попутно логичную вещь – коэффициенты итогового уравнения, «отвечающие» за поворот и параллельный перенос равны нулю: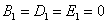

Поскольку инварианты (числа) 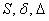НЕ ЗАВИСЯТ от коэффициентов того или иного уравнения, которым задана конкретная исследуемая линия, то справедливыми являются следующие равенства:

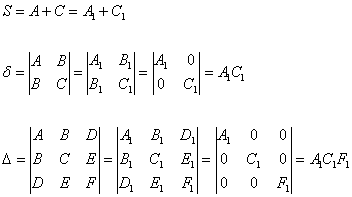
откуда следует простой и изящный алгоритм решения нашей задачи:

1) Из исходного уравнения находим числа .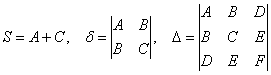
2) Решаем систему 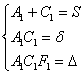и записываем уравнение 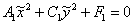, которое легко приводится к каноническому виду. При этом координаты 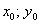нового начала координат 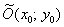отыскиваются как решение системы линейных уравнений 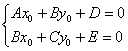, а угол «альфа» поворота новой системы координат 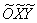относительно старой системы координат 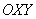– из уравнения 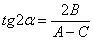. Если 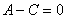, то .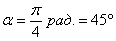

Таким образом, решение нашей задачи укладывается в стройную и понятную схему, доступную даже школьнику. Выясним же, наконец, как из потрёпанного уравнения 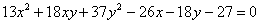получается канонический эллипс :

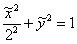Пример 1

Привести уравнение линии второго порядка к каноническому виду

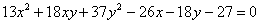
Найти начало соответствующей системы координат и угол её поворота

Решение: перейдём к новой прямоугольной системе координат 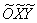, в которой уравнение данной линии примет вид .

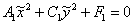На первом шаге из исходного уравнения находим коэффициенты .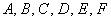
В тетради это удобно сделать следующим образом:

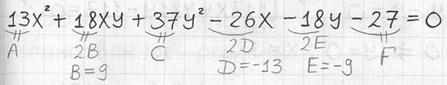
Здесь важно не потерять «минусы», а также не забыть разделить пополам нужные числа. Кроме того, некоторые слагаемые уравнения 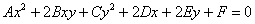могут отсутствовать, и тогда соответствующие коэффициенты будут равны нулю – не спешим и не путаемся!

В нашем случае всё на месте и, соответственно, все коэффициенты ненулевые:

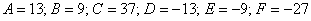
Вычислим инварианты:

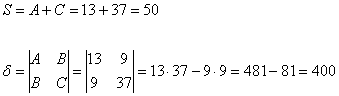
Последний определитель выгодно раскрыть с помощью элементарного преобразования, прибавив к третьей строке первую строку:

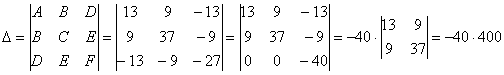
Инварианты найдёны, составим и решим систему:

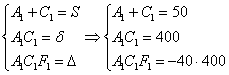
Из последних двух уравнений сразу просматривается значение коэффициента :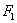
поскольку 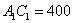, то, подставляя это произведение в 3-е уравнение, получаем:

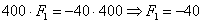
Но его обычно оставляют на закуску, тут важно разобраться с другими коэффициентами. Есть длинный путь, и есть короткий путь.

Путь длинный: из 1-го уравнения выражаем 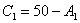– подставляем во второе уравнение:

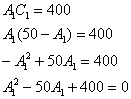
Решим квадратное уравнение:

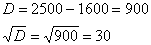
В результате получается два комплекта симметричных корней:

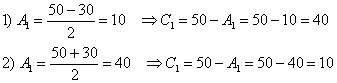
Путь короткий, к которому я рекомендую пристреляться, в том числе, и чайникам. Это подбор корней. Смотрим на первые два уравнения системы: 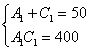. Прикидку можно делать либо по первому уравнению, либо по второму, кому как удобнее. Лично я привык ориентироваться по сумме коэффициентов. Правдоподобных вариантов здесь не так и много:
0 и 50
10 и 40 – удовлетворяет и первому и второму уравнению
20 и 30
30 и 20
40 и 10 – симметричная пара корней
50 и 0

Как видите, на подходящую пару чисел мы «натыкаемся» практически сразу. В силу симметричности уравнений решением будут являться и «зеркальные» значения 40 и 10.

Таким образом, в нашем распоряжении оказывается два набора корней:

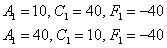
Не забываем выполнить проверку, подставив значения первого (можно второго) комплекта в левую часть каждого уравнения системы:

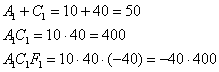
Получены соответствующие правые части исходных уравнений, что и требовалось проверить.

Теперь мысленно либо на черновике следует выяснить, какое решение приведёт нас к желаемому результату.

Подставляем 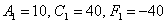в уравнение :

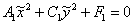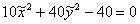
Техника завершающих преобразований хорошо знакома из предыдущих уроков об эллипсе, гиперболе и параболе:

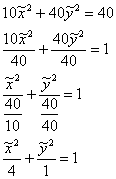
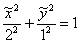– эллипс с центром в точке 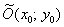, большой полуосью 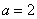, малой полуосью .

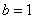Такой фразы будет достаточно – нас никто не спрашивал про фокусы, эксцентриситет и другие характеристики линии.

Всё вышло удачно с первой попытки. Если в уравнение 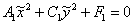подставить второй набор корней 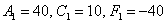, то получится неканоническая запись того же эллипса 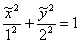– повернутого на 90 градусов (уже в новой системе координат). Случай такого поворота я рассмотрел ещё в ознакомительных материалах про эллипс.

Координаты 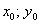начала новой системы координат 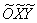найдём как решение системы:

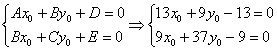
Первое уравнение умножим на 9, второе уравнение умножим на 13 и из 2-го уравнения почленно вычтем 1-ое (проще способа не видно):

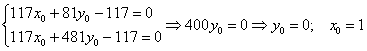
Таким образом: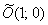

Найдём угол поворота новой системы координат 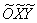относительно старой:

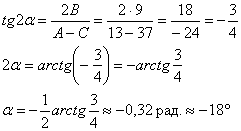
В том случае если по условию необходимо выполнить чертёж – выполняем чертёж, приведённый в начале урока. Впрочем, мне нетрудно скопипастить:

Ввиду сложности чертежа вполне допустимо его схематичное оформление, однако всё-таки постарайтесь, чтобы рисунок был похож на правду.

В лайт-варианте можно изобразить только систему координат 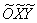и эллипс в «нормальном» положении, но тогда могут возникнуть вопросы у преподавателя. Да, и ещё момент – при таких раскладах координаты центра запишутся в новой системе координат: 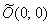, что вызовет дополнительную путаницу.

Ответ: 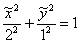– эллипс с полуосями 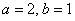– в системе координат 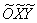с началом в точке 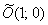, повёрнутой относительно исходной системы координат 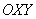на угол .

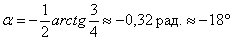Это мы рассмотрели так называемый эллиптический случай, когда коэффициенты 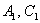– отличны от нуля и одного знака (оба положительны либо оба отрицательны), т.е. когда их произведение .

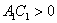Но при таком раскладе может получиться не только эллипс. Если все три коэффициента 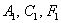одного знака, то получится мнимый эллипс. Условно говоря, если бы мы в рассмотренной задаче получили уравнение 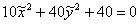, то пришли бы к уравнению 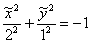. Причём, весь алгоритм и порядок оформления остались бы прежними + приятный бонус – отсутствие чертежа, поскольку мнимый эллипс остаётся разве что мнить =)

Ещё одна разновидность эллиптического случая – нулевой свободный член: 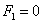, предвестником которого является нулевой третий инвариант 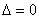. И действительно, из 3-его уравнения системы 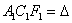следует, что есл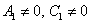и и 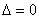, то нулю может быть равен только коэффициент «эф первое». Условно говоря, в нашей задаче получилось бы уравнение 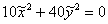, которое легко сводится к пункту №6 классификации линий 2-го порядка: 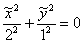– пара мнимых пересекающихся прямых с единственной действительной точкой их пересечения 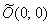– с нулевыми координатами новой системы координат .

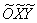Предлагаю самостоятельно ознакомиться с гиперболическим случаем:

Пример 2

Привести уравнение линии второго порядка к каноническому виду

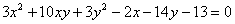
Найти начало соответствующей системы координат, угол её поворота и выполнить чертёж.

После краткого образца решения есть важные дополнительные комментарии.

Во второй части статьи рассмотрим параболический случай 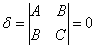, где по очевидной причине метод инвариантов становится непригодным:

Date: 2015-04-23; view: 2280; Нарушение авторских прав