Директрисы гиперболы

У гиперболы, точно так же, как у эллипса, две директрисы. В каноническом случае 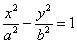они расположены между ветвями гиперболы и задаются такими же уравнениями 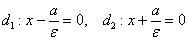, где «эпсилон» эксцентриситет данной гиперболы.

В рассматриваемом примере:

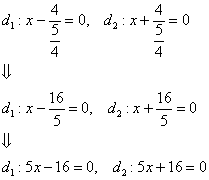
Более того, для гиперболы справедлива абсолютно такая же теорема:

Гипербола – есть множество всех точек плоскости, таких, что отношение расстояния до каждой точки от фокуса к расстоянию от неё до соответствующей (ближайшей) директрисы равно эксцентриситету:

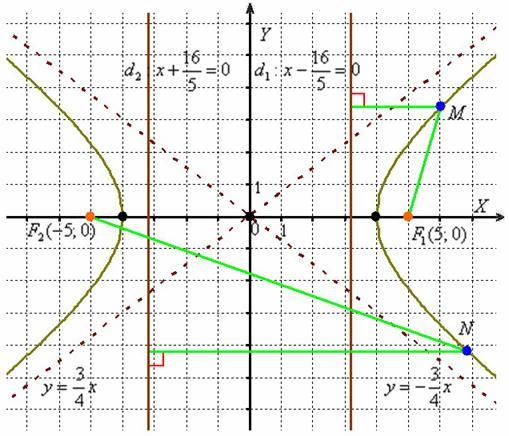
То есть, для любой точки 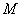гиперболы отношение её расстояния от фокуса 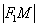к расстоянию от неё же до ближайшей директрисы 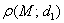равно эксцентриситету: .

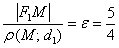Для пары 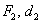и любой точки 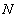гиперболы (ради разнообразия я выбрал демонстрационную точку дальней ветви) отношение такое же:

К слову, у параболы с её единственным фокусом и единственной директрисой по определению эти длины относятся «один к одному», поэтому эксцентриситет любой параболы и равен единице.

Ответ: искомая линия представляет собой гиперболу 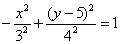с центром симметрии в точке 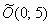и повёрнутую на 90 градусов относительно своего канонического положения. Канонический вид уравнения: 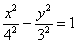, фокусы: 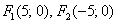, эксцентриситет: 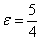, асимптоты: 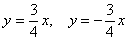, директрисы: .

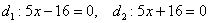Очень хотелось упростить пример, но он взят из конкретной работы, поэтому пришлось с упорным занудством разобрать все-все-все тонкости и технические приёмы. Налью всем по стакану молока за вредность и подкину задание для самостоятельного решения:

Задача 8

Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки 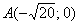к расстоянию до прямой 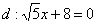постоянно и равно 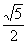. Сделать точный чертеж.

Подумайте, о какой это точке и о какой прямой шепчет условие;-)

Героически разбираемся с решением и чертежом, после чего с чистой душой и лёгким сердцем засыпаем на раскладушках возле мониторов, чтобы проснуться к следующиму занятию со свежими головами и розовыми лицами.

Спокойной ночи!

Решения и ответы:

Пример 2: Решение: Пусть точка 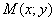принадлежит искомому множеству точек. Тогда:


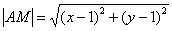
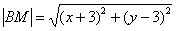
По условию:

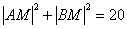
Или:

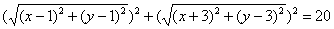
Упростим уравнение:

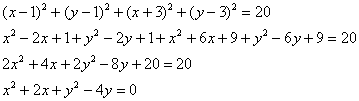
Выделим полные квадраты:

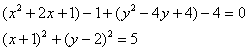
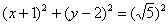– окружность с центром в точке 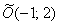радиуса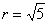
Выполним чертеж:

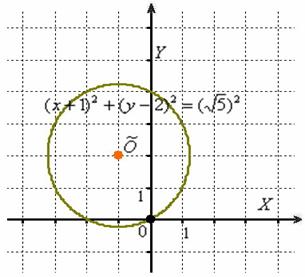
Приведём уравнение к каноническому виду.
1) Способ первый. Осуществим параллельный перенос окружности центром в начало координат: .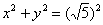
2) Способ второй. С помощью параллельного переноса перейдём от исходной к новой прямоугольной системе координат 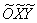с началом в точке . Таким образом, уравнение окружности запишется в каноническом виде: .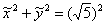
Ответ: уравнение искомого множества точек 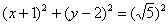задаёт окружность с центром в точке 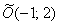радиуса 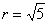. Канонический вид уравнения: 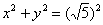(или 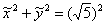в зависимости от способа). Фокусы окружности совпадают и находятся в её центре. У окружности отсутствуют асимптоты. Эксцентриситет любой окружности равен нулю.

Пример 4: Решение: пусть точка 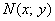принадлежит искомому множеству точек. Тогда:

По условию:

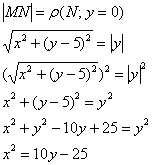
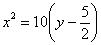– парабола, ветви которой направлены вверх, с вершиной 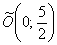и фокальным параметром :

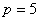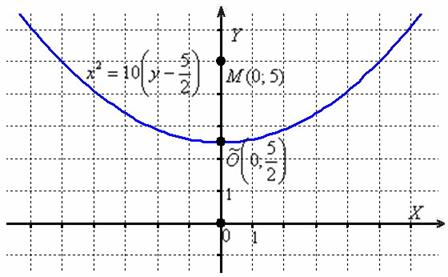
Примечание: аналитическое условие задачи формулирует определение данной параболы, т.е. точка является её фокусом, а ось абсцисс – директрисой.
Приведём уравнение кривой к каноническому виду:
1) Повернём параболу 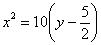на 90 градусов по часовой стрелке вокруг вершины 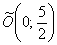: 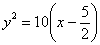и осуществим её параллельный перенос вершиной в начало координат: .
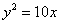2) Повернём прямоугольную систему координат 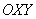на 90 градусов против часовой стрелки и перенесём её началом координат в точку 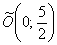. Тогда в новой системе координат 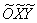уравнение данной параболы примет канонический вид .
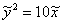Ответ: 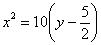– парабола. Каноническое уравнение: 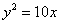(либо 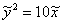в зависимости от способа приведения).

Пример 6: Решение: пусть точка принадлежит искомому множеству точек. Тогда:

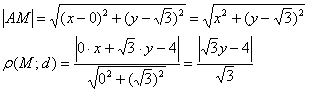
По условию:

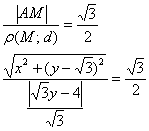
Приведем уравнение к каноническому виду:

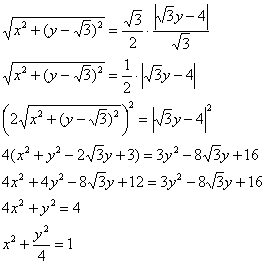
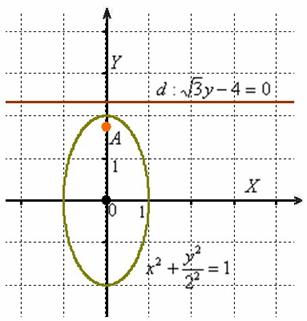
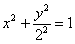– эллипс с центром в начале координат и полуосями, равными 1 и 2.
Примечание: здесь нежелательна формулировка «с полуосями », поскольку буквой «а» стандартно обозначают большую полуось, а «единица» таковой не является по причине неканонического положения эллипса.
Выполним чертеж:

Приведём уравнение к каноническому виду:
1) Способ первый. Повернём эллипс вокруг центра на 90 градусов: .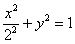
Вычислим 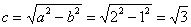и запишем фокусы:
.
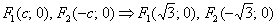Найдём эксцентриситет: .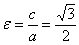
Директрисы эллипса задаются уравнениями 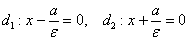, в данном случае:

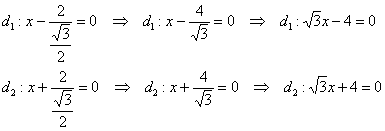
Ответ: искомое множество точек представляет собой эллипс 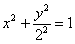. Канонический вид уравнения: 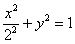. Фокусы: 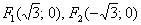, эксцентриситет: 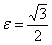, директрисы: .

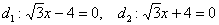2) Способ второй. Используем поворот координатных осей на 90 градусов против часовой стрелки, то есть, перейдём к новой системе координат 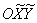(ось 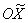совпадёт с осью 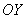старой системы координат, а ось 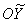будет противоположно направлена к оси 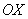). Тогда: .
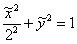! Все дальнейшие действия проводятся в новой системе координат – с переменными !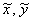
Вычислим 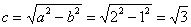и запишем фокусы эллипса:
.
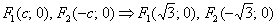Эксцентриситет: .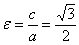
Директрисы эллипса задаются уравнениями 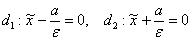, в данном случае:

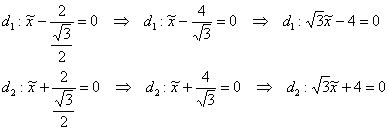
Ответ: искомое множество точек представляет собой эллипс 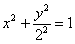. Канонический вид уравнения: 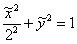. Фокусы: 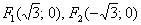, эксцентриситет: 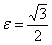, директрисы: .

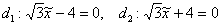Пример 8: Решение: Пусть точка 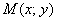принадлежит искомому множеству точек. Тогда:
,
.
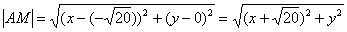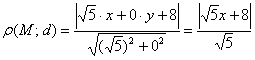По условию:

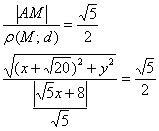
Упростим уравнение:

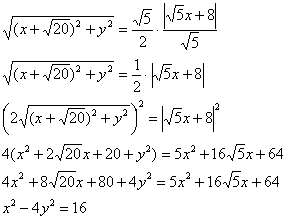
– каноническое уравнение гиперболы с действительной полуосью 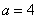, мнимой полуосью .
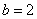Выполним чертёж:

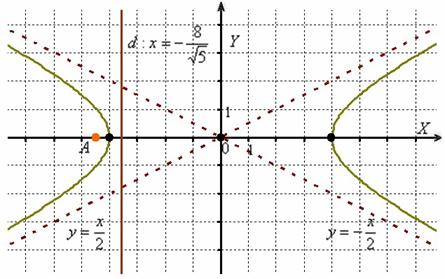
Ответ:
Примечание: точка 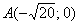является вторым фокусом гиперболы, прямая 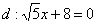– второй директрисой, а их отношение 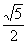– эксцентриситетом.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?