Понятие скалярного произведения

Сначала про угол между векторами. Думаю, всем интуитивно понятно, что такое угол между векторами, но на всякий случай чуть подробнее. Рассмотрим свободные ненулевые векторы 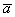и 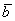. Если отложить данные векторы от произвольной точки 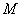, то получится картинка, которую многие уже представили мысленно:

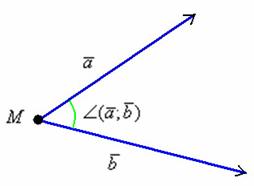
Признаюсь, здесь я обрисовал ситуацию только на уровне понимания. Если необходимо строгое определение угла между векторами, пожалуйста, обратитесь к учебнику, для практических же задач оно нам, в принципе, ни к чему. Также ЗДЕСЬ И ДАЛЕЕ я буду местами игнорировать нулевые векторы ввиду их малой практической значимости. Оговорку сделал специально для продвинутых посетителей сайта, которые могут меня упрекнуть в теоретической неполноте некоторых последующих утверждений.

Угол между векторами 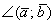может принимать значения от 0 до 180 градусов (от 0 до 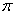радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства: 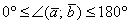либо 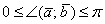(в радианах).

В литературе значок угла 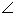часто пропускают и пишут просто .

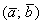Определение: Скалярным произведением двух векторов 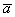и 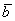называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними:

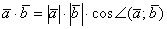
Вот это вот уже вполне строгое определение.

Акцентируем внимание на существенной информации:

Обозначение: скалярное произведение обозначается через 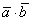или просто .

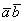Результат операции является ЧИСЛОМ: Умножается вектор на вектор, а получается число. Действительно, если длины векторов 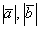– это числа, косинус угла – число, то их произведение 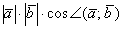тоже будет числом.

Сразу пара разминочных примеров:

Пример 1

Найти скалярное произведение векторов 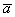и 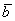, если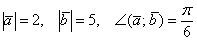

Решение: Используем формулу 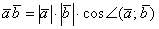. В данном случае:

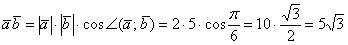
Ответ: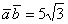

Значения косинуса можно найти в тригонометрической таблице. Рекомендую её распечатать – потребуется практически во всех разделах вышки и потребуется много раз.

Чисто с математической точки зрения скалярное произведение безразмерно, то есть результат, в данном случае 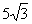, просто число и всё. С точки же зрения задач физики скалярное произведение всегда имеет определенный физический смысл, то есть после результата нужно указать ту или иную физическую единицу. Канонический пример по вычислению работы силы можно найти в любом учебнике (формула в точности представляет собой скалярное произведение). Работа силы измеряется в Джоулях, поэтому, и ответ запишется вполне конкретно, например, .

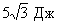Пример 2

Найти 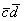, если 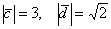, а угол между векторами равен .

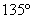Это пример для самостоятельного решения, ответ в конце урока.

Date: 2015-04-23; view: 685; Нарушение авторских прав