Последовательности натуральных чисел

Натуральное число является количественной характеристикой одного неизменного множества, однако, на практике количество предметов постоянно меняется, например, поголовье скота в некотором хозяйстве. Более того, простейшая, но и важнейшая последовательность сразу же возникает в процессе счёта – это последовательность натуральных чисел: 1, 2, 3, ….

Если изменение количества предметов в некоторой совокупности зафиксировано в виде некоторой последовательности натуральных чисел (членов последовательности), тут же естественным образом возникает ещё одна последовательность – последовательность номеров, например

В связи с этим возникает проблема обозначения членов последовательности. Обозначение каждого члена особой буквой крайне неудобно по следующим причинам. Во-первых, последовательность может содержать очень большое, или даже бесконечное число членов. Во-вторых, разные буквы скрывают тот факт, что члены последовательности относятся к одной совокупности, хотя и меняющей количество элементов. Наконец, в этом случае не будут отражены номера членов в последовательности.

Эти причины заставляют обозначать члены последовательности одной буквой и различать их по индексу. Например, последовательность, состоящую из десяти членов, можно обозначить буквой а: а ₁, а ₂, а ₃, …, а ₁₀. Тот факт, что последовательность является бесконечной, выражается многоточием, как бы неограниченно продлевающим эту последовательность: а ₁, а ₂, а ₃, … Иногда последовательность начинают нумеровать с нуля:: а ₀, а ₁, а ₂, а ₃, …

Некоторые последовательности могут восприниматься как случайные наборы чисел, поскольку не известен, или вообще отсутствует, закон формирования членов последовательности. Однако особое внимание привлекают последовательности, для которых такой закон известен.

Для указания закона формирования членов последовательности чаще всего используются два способа. Первый из них состоит в следующем. Задается первый член, а затем указывается способ, согласно которому с помощью последнего, уже известного члена получается следующий. Для записи закона используется член последовательности с неопределённым номером, например, а_k и следующий за ним член а_k+1, после чего записывается связывающая их формула.

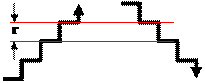Наиболее известными и важными примерами могут послужить арифметическая и геометрическая прогрессии. Арифметическая прогрессия определяется формулой а_k+1 = а_k + r (либо а_k+1 = а_k – r). Члены арифметической прогрессии либо равномерно растут (лесенкой), либо равномерно убывают (тоже лесенкой). Величина r называется разностью прогрессии, поскольку а_k+1 – а_k = r. Примерами арифметических прогрессий с натуральными членами являются

а) натуральные числа (а₁ = 1; а_k+1 = а_k + 1);

б) бесконечная последовательность 1, 3, 5, 7, … (а₁ = 1; а_k+1 = а_k + 2);

в) конечная последовательность 15, 12, 9, 6, 3 (а₁ = 15; а_k+1 = а_k – 3).

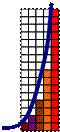Геометрическая прогрессия определяется формулой b_k+1 = b_k∙q. Величина q называется знаменателем геометрической прогрессии, поскольку b_k+1:b_k = q. Геометрические прогрессии с натуральными членами и знаменателем, превосходящим единицу, растут и растут быстро, даже лавинообразно. Примерами геометрических прогрессий с натуральными членами являются

а) бесконечная последовательность 1, 2, 4, 8, … (b₁ = 1; b_k+1 = b_k∙2);

б) бесконечная последовательность 3, 12, 48, 192, 768,… (b₁ = 3; b_k+1 = b_k∙4).

Второй способ указания закона определения членов последовательности состоит в указании формулы, позволяющей вычислить член последовательности с неопределённым номером (общий член), например, а_k, с помощью номера k.

Члены арифметической и геометрической прогрессий можно вычислять и этим способом. Поскольку арифметическая прогрессия определяется формулой а_k+1 = а_k + r, легко понять, как выражается член а_k с помощью номера k:

а₁ – определён произвольно;

а₂ = а₁ + r= а₁ + 1∙r;

а₃ = а₂ + r = а₁ + r + r = а₁ + 2∙r;

а₄ = а₃ + r = а₁ + 2∙r + r = а₁ + 3∙r;

…………………………………

а_k = а₁ + (k – 1)∙r – итоговая формула.

Для геометрической прогрессии аналогичным способом выводится формула общего члена: b_k = b₁ ∙ q^{k – 1} .

Кроме арифметической и геометрической прогрессий таким же способом можно определить другие последовательности, имеющие особый характер изменения. В качестве примера приведём последовательность квадратов натуральных чисел: s_k = k ²: 1² = 1, 2² = 4, 3² = 9, 4² = 16, 5² = 25…

Существуют более сложные способы образования последовательностей, например, одна строится с помощью другой. Особое значение для арифметики имеет геометрическая прогрессия, определяемая параметрами b₁ = 1, q = 10, то есть последовательность степеней десятки: 1 = 10⁰, 10 = 10¹, 10², 10³, …, 10^k, … Она используется для представления натуральных чисел в позиционной системе счисления. При этом для каждого натурального числа n возникает последовательность, состоящая из цифр, с помощью которых записывается данное число: а_n а_{n – 1} … а₂ а₁ а₀. Цифра а_k указывает сколько слагаемых типа 10 ^k содержит число n.

Понятие последовательности подводит к важнейшим для математики понятиям величины и функции. Величина – это изменяющаяся числовая характеристика какого-то предмета или явления. Её изменение воспринимается как последовательность чисел. Существование зависимости между самими членами и их номерами, а также её выражение с помощью формул вплотную подводит к понятию функции.

Важнейшим математическим открытием, которое используется практически каждым членом достаточно развитого общества, является позиционная система счисления. Она позволила решить основную проблему счёта, состоящую в умении называть все новые и новые числа, используя обозначения (цифры) только для нескольких первых чисел.

Позиционная система счисления традиционно связана с числом десять, но на тех же принципах можно построить и иные системы, например, двоичную. При построении десятичной позиционной системы счисления вводятся десять арабских цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью может быть записано число, выражающее количество предметов любого конечного множества. Для этой цели используется специальный алгоритм, то есть чётко определённая последовательность элементарных действий.

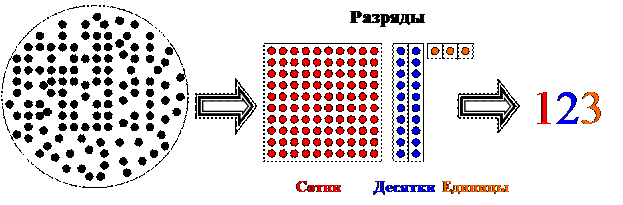
Пересчитываемые предметы объединяются в группы по десять, что соответствует делению на десять с остатком. В результате образуются два множества – единиц и десятков. Десятки снова группируются по десять в сотни. Ясно, что число десятков (обозначим его через а₁) обязательно меньше десяти, и, значит, а₁ можно обозначить цифрой. Далее сотни группируются в тысячи, тысячи – в десятки тысяч и т. д. пока все предметы не будут сгруппированы. Построение числа завершается тем, что слева направо записываются полученные цифры от больших индексов к меньшим. Цифре а_k соответствуют количество групп предметов по 10 ^k. Итоговая запись числа состоит из конечной последовательности цифр а_n а_{n – 1} … а₂ а₁ а₀. Соответствующее число равно выражению

а_n·10ⁿ + а_{n – 1}·10^{n – 1} + … + а₂·10² + а₁·10¹ + а₀·10⁰.

Слово «позиционная» в названии системы счисления связано с тем, что цифра меняет свой смысл в зависимости от своей позиции в записи числа. Последняя цифра задаёт число единиц, предпоследняя – число десятков и т. д.

Отметим, что алгоритм для получения записи чисел в системе счисления с любым основанием N: состоит в последовательной группировке предметов по N штук. При записи числа необходимо использовать N цифр.

С помощью позиционной системы счисления можно записать любое число, но назвать его по правилам русского языка бывает затруднительно, поскольку нужны новые названия для степеней десятки. Для практических нужд используются миллионы (10⁶), миллиарды (10⁹), триллионы (10¹²). Для указания порядка очень больших чисел проще указывать максимальную степень десятки.

Date: 2015-05-04; view: 2088; Нарушение авторских прав