Ассоциативность Коммутативность Ассоциативность Суммирование

Для умножения также действуют законы коммутативности и ассоциативности, выражаемые равенствами a b = b a и(a b) с = a (b с).

Для обоснования этих правил следует использовать геометрическое истолкование умножения. При многократном сложении (b раз) нескольких равных куч (по a предметов), можно заменить каждую кучу полосой из a единичных квадратов и сложить b полос одну под другой. В итоге получится прямоугольник a на b, площадь которого равна a b. Его можно повернуть на 90º и представить, что он сложен из a горизонтальных полос, содержащих по b единичных квадратов. Площадь его не изменилась, следовательно, a b = b a.

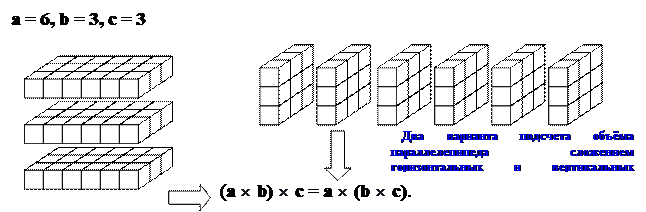
При рассмотрении произведения трёх чисел a b с предметы можно заменить единичными кубами и сложить из них параллелепипед. Его можно сложить из с горизонтальных пластин размером a на b, или же из а вертикальных пластин размером b на с. Произведение a b с равно объёму параллелепипеда, а, значит, (a b) с = a (b с). Так же как и в случае сложения, закон ассоциативности позволяет использовать запись произведения нескольких сомножителей вообще без скобок.

Как и в случае сложения, практическая важность законов коммутативности и ассоциативности при нахождении произведения связана с тем, что процесс перемножения чисел порой упрощается при изменении порядка вычислений, например, 5 ∙ 59 ∙ 4 = 5 ∙ (59 ∙ 4) = 5 ∙ (4 ∙ 59) = (5 ∙ 4) ∙ 59 = 20 ∙ 59 = 1180.

Date: 2015-05-04; view: 835; Нарушение авторских прав