Простейшие неравенства

Неизвестные величины могут встречаться и в неравенствах. Простейшие неравенства имеют вид x < a или x > b. Первое из них имеет или конечное число решений х = 1, 2, … а – 1 (если а больше единицы), или вообще не имеет натуральных решений (если а равно единице). Неравенство второго типа имеет бесконечное число решений: х = b + 1, b + 2, …

Графически можно проиллюстрировать неравенства вида x < a и x > b следующим образом.

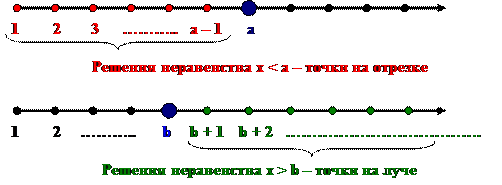Решить более сложное неравенство – привести его к простейшему виду. Характер преобразований, производимых над неравенствами таков же, как и при преобразованиях равенств и уравнений.

Рассмотрим, например, неравенство 7 + х < 15. Смысл преобразований, необходимый для решения неравенства, таков. Если одно число меньше другого, то при вычитании из них одного и того же числа неравенство не нарушится. Следовательно, из исходного неравенства 7 + х < 15 следует другое равенство: (7 + х) – 7 < 15 – 7 или х < 8. Таким образом, решением неравенства являются натуральные числа х = 1, 2, 3, 4, 5, 6, 7.

Можно рассматривать неравенства более чем с одним неизвестным. В качестве примера решим неравенство х∙у > x + y. Для этого проведём следующие рассуждения, используя геометрическое истолкование произведения.

Числа х и у либо равны, либо одно из них больше другого. Пусть для определённости х ≥ у. Геометрически умножение числа х на число у связано с последовательным прикладыванием в виде прямоугольника друг к другу горизонтальных полос, содержащих по х квадратов. Если у ≥ 2, то прямоугольник заведомо содержит две полосы, состоящих из 2 ∙х квадратов, то есть х∙у ≥ 2∙х.

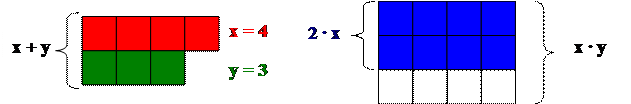Поскольку х ≥ у, получаем, что 2∙х ≥ x + y. Если же х > у, то 2∙х > x + y. Итак, если х > у и у ≥ 2, то х∙у ≥ 2∙х > x + y. Таким образом, все пары чисел х и у, таких, что х > 2 и у ≥ 2, являются решениями неравенства. Остаётся рассмотреть варианты: а) х = 2 и у = 2 – не является решением; б) х – любое и у = 1 – не является решением, так как х∙1 = х < x + 1.

Date: 2015-05-04; view: 812; Нарушение авторских прав