Ассоциативность Коммутативность Ассоциативность Умножение

Используя законы умножения, можно получить некоторые свойства операции деления. Пусть, a = b с d, тогда a = (b с) d, то есть a: (b с) = d. С другой стороны (a: b): с = (с d): с = d, то есть (a: b): с = a: (b с).

Наличие геометрического истолкования умножения и его большая практическая важность указывает на существование глубокой связи числовых отношений и простых геометрических форм. По крайней мере, становится ясным, что истолкование смысла арифметических операций хотя бы отчасти связано с упорядоченным расположением предметов в пространстве.

4.

Геометрическое истолкование умножения позволяет понять смысл закона, связывающего операции сложения и умножения. Речь идёт о законе дистрибутивности.

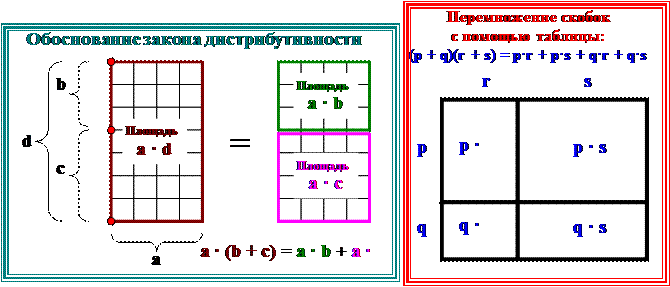Произведение чисел a и d можно рассматривать как выражение для площади прямоугольника со сторонами a и d. Разобьём сторону длиной d на две части, длины которых обозначим через b и c (таким образом, d = b + c). Исходный прямоугольник будет разбит на две части, сумма площадей которых как раз и равна площади исходного прямоугольника. Символически это обстоятельство можно записать в виде равенства a · (b + c) = a · b + a · c, которое выражает закон дистрибутивности.

Закон дистрибутивности позволяет перемножать скобки, содержащие любое количество слагаемых. При этом могут использоваться два подхода. Первый состоит в том, что исходное выражение преобразуется по законам коммутативности, ассоциативности и дистрибутивности. В этом состоит основной принцип алгебраических вычислений, приводящий к выводу новых формул. Приведём пример перемножения двух скобок, содержащих по два слагаемых:

(p + q) · (r + s) = (p + q) · r + (p + q) · s = r · (p + q) + s · (p + q) =

r · p + r · q + s · p + s · q

Второй подход основан на геометрическом истолковании умножения. Одну сторону прямоугольника разбивают на отрезки, число которых равно числу слагаемых в первой скобке, и возле каждого отрезка записывают одно из этих слагаемых. Со второй стороной прямоугольника поступают аналогично, применительно ко второй скобке. Проводя через точки деления вертикальные и горизонтальные линии, разбивают исходный прямоугольник на малые прямоугольники, в каждый из которых вписывают его площадь, равную произведению длин его сторон. Можно сказать, что исходный прямоугольник превратится в таблицу, клетками которой являются малые прямоугольники. Площадь большого прямоугольника одновременно равна произведению скобок и сумме малых прямоугольников. В итоге можно сформулировать правило: произведение скобок равно сумме всех попарных произведений каждого слагаемого из первой скобки на каждое слагаемое второй скобки.

5.

По определению aⁿ = а · а · а · … · а · а (читается: а в степени n).

Особые названия, связанные с геометрическим истолкованием произведения, имеют степени a² – квадрат, a³ – куб, a⁴ – биквадрат (двойной квадрат).

Символически обозначив операцию возведения в степень и получаемый при этом результат с помощью равенства aⁿ = c, мы можем перечислить соответствующие термины, используемые в арифметике:

а – основание степени, n – показатель степени, с – степень (n -я).

Легко понять, что а ≥ с, при этом равенство возможно только при а =1.

1. aⁿ ∙ a^m = а · а · а · … · а · а · а · а · а · … · а · а = a^n+m.

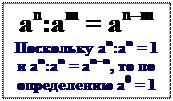
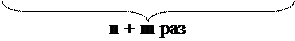Таким образом, при перемножении степеней с равными основаниями показатели степеней складываются.

2. Аналогично доказывается, что при делении степеней с равными основаниями показатели степеней вычитаются (n > m).

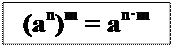
3. 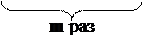(aⁿ)^m = · аⁿ · аⁿ · …· аⁿ · аⁿ = а · а · а · … · а · а = a^n∙m.

При возведении степени в степень показатели степеней перемножаются.

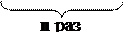
4. aⁿ ∙ bⁿ = а · а · … · а · a · b · b · … · b · b = (ab)ⁿ.

При перемножении степеней с равными показателями основания степени перемножаются.

Если заданы основание степени а и показатель степени n, то мы можем вычислить соответствующую степень aⁿ = c. Иногда возникает обратная задача: заданы степень с и её показатель n, нужно определить основание степени а. Поскольку пока мы говорим только о натуральных числах, искомое число а можно вычислить, перебрав все n -е степени натуральных чисел от 1 до с, то есть числа 1 ⁿ, 2 ⁿ, … cⁿ, и сравнив их с числом с. Если одно из них (aⁿ) совпадёт с с, то основание степени (а) найдено. Говорят, что а является корнем n -й степени из числа с. Это обстоятельство выражают записью: 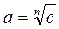. В случае когда n = 2, корень называют квадратным и не указывают степень: 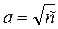. Корень третьей степени называют кубическим. Для произвольных натуральных чисел с и n операция извлечения корня (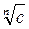) выполняется далеко не всегда, например, не существует натурального числа а, равного .

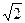Из свойств степеней вытекают некоторые свойства корней:

, , .

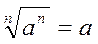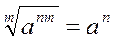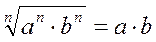6.

Геометрически натуральные числа принято изображать как уходящую в бесконечность последовательность равноотстоящих друг от друга точек, расположенных на луче. Данный образ хорошо передаёт суть счёта как последовательного перечисления однородных предметов, связанного с движением во времени. Здесь наглядно проявляется тот факт, что числами (и числительными) обозначается не только количество предметов, но и их порядок при счёте.

Понятие порядка является одним из важнейших в математике. Первым из натуральных чисел является единица, а каждое последующее число получается из предыдущего с помощью добавления единицы: 1, 2 = 1+ 1, 3 = 2 + 1 и т. д. Таким образом, чем больше натуральное число, тем дальше оно расположено от начала луча. Для обозначения порядка чисел и их относительной величины используются символы n < m (меньше), n ≤ m (меньше или равно), n > m (больше), n ≥ m (больше или равно), n = m (равно).

Геометрическое изображение натуральных чисел точками луча указывает на связь счёта с измерением отрезков. Фактически числовой луч превращён в линейку и позволяет измерить любой приложенный к ней отрезок и выразить его длину целым числом. Вообще же измерение отрезков является одной из самых естественных операций – речь идёт о подсчёте шагов при ходьбе.

Очень близкой к операции измерения отрезков является операция сравнения длины отрезков. Пусть, например, заданы два уже измеренных отрезка, длины которых равны n и m соответственно. Откладывая второй отрезок вдоль первого, можно установить, сколько раз он укладывается в первый и какой при этом остаётся остаток. Данная процедура даёт геометрический образ деления натуральных чисел с остатком.

Деление с остатком можно понимать как разбиение исходного множества из n элементов на два новых множества. Первое множество состоит из r элементов исходного множества, а второе состоит из q элементов, каждый из которых сам по себе является множеством, содержащим m элементов исходного. Если положить m равным десяти, мы придём к операции разбиения множества на десятки, что является важнейшим действием при записи чисел в десятичной системе счисления.

Простой способ деления числа n на число m с остатком таков. Из кучи, содержащей n предметов, последовательно удаляют совокупности по m предметов, считая число удалений (q), пока не останется r предметов, где r < m.

Date: 2015-05-04; view: 1698; Нарушение авторских прав