Экстремум функции

Определение 74. Точка 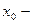точка строгого локального максимума (минимума) функции f(x), если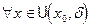

f(x) < f(x₀) (f(x) > f(x₀)) при 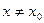. В случае экстремума функции: 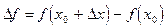= f(x) - f(x₀) < 0 (максимум),

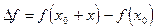= f(x) - f(x₀) > 0 (минимум).

Локальный максимум или локальный минимум называются локальными экстремумами. Точки возможного экстремума функции называются стационарными.

Теорема 47. (необходимое условие экстремума).

Пусть 1)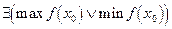

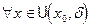
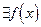
2)

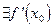
Тогда 1),2) .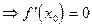

Доказательство. Так как 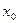- точка локального экстремума,

то 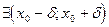, где 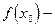наибольшее или наименьшее

значение, тогда по теореме Ферма . ¨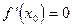

Геометрический смысл теоремы.

В точках возможного экстремума касательные к графику функции параллельны оси Ох.

Примечание 1. Равенство 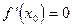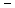лишь необходимое условие экстремума.

Пример 94. 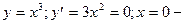не точка экстремума.

Примечание 2. Экстремум функции может существовать и в точке, где функция не имеет производной.

Пример 95. 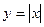. В точке х=0 экстремум функции, но производная в этой точке не существует.

Теорема 48. (достаточное условие строгого экстремума).

Пусть 1) $f(x) "xÎU(x₀, d)

2) f(x)ÎС¹(U(x₀, d))

(в точке 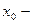функция может быть не дифференцируемой).

Тогда 1)2)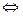

f(x₀) =

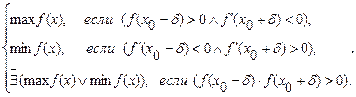
Доказательство. Воспользуемся формулой Тейлора для функции 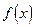в точке :

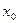В формуле учтено, что 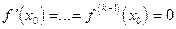. Остаток

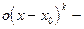более высокого порядка малости, чем

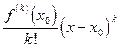, поэтому знак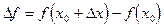

совпадает со знаком 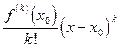. При четном 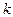зна-

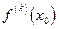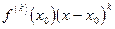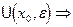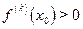
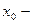ки и совпадают в при точка локального минимума и при

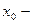точка локального максимума.

Если 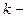нечетное, то из совпадения знаков чисел

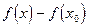и 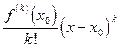следует 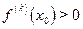. Раз

ность 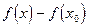положительна при 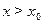и отрицательна

при 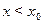. Функция возрастает в точке 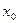при

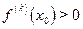и убывает при . ¨

Пример 95. Найти экстремум функции y = f(x) = x².

Решение. Найдем стационарные точки y¢ = 2x = 0. Точка x = 0 -стационарная точка. Производная меняет знак с минуса на плюс. Следовательно, х = 0 - точка минимума функции.

Пример 96. Найти наибольшее и наименьшее значения функции

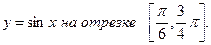
Решение.

найдем критические точки

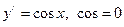, решая уравнение, находим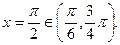

вычислим значения функции в критических точках и на концах отрез

ка

.

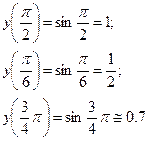наибольшее значение данной функции на отрезке равно 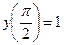, наименьшее -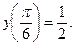

Примечание 1. Если производная 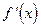не меняет знака, то 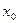не является точкой экстремума.

Пример 97. Найти экстремум функции y = x³.

Решение. Найдем стационарную точку у' = 3х² = 0. Точка х=0-стационарная точка. Производная во всех точках неотрицательна и не меняет знака при переходе через точку х=0. Точка х=0 не является точкой экстремума.

Примечание 2. Теорема остается справедливой, если функция 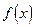в самой точке 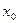не дифференцируема, а только непрерывна.

Пример 98. 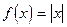в точке 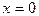непрерывна, но не дифференцируема.

Date: 2015-06-08; view: 672; Нарушение авторских прав