Тема: Непрерывность функции

1. Контрольные вопросы:

1. Какая функция называется непрерывной в точке?

______________________________________________________________________________________________________________________________________________________________________________________________________

2. Какая функция называется непрерывной на промежутке?

______________________________________________________________________________________________________________________________________________________________________________________________________

3. Функция в точке х₀ терпит разрыв, если: (укажите характер точек разрыва)

а)___________________________________________________________________________________________________________________________________б)___________________________________________________________________________________________________________________________________

в)___________________________________________________________________________________________________________________________________

4. Сформулируйте свойства функции непрерывной в точке:

______________________________________________________________________________________________________________________________________________________________________________________________________

5. Сформулируйте свойства функции непрерывной на промежутке:

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

6. Сформулируйте алгоритм исследования функции на непрерывность и выявления точек разрыва (указать их характер)

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2. Практические задания по теме:

Задание 1. Для функции у=f(x) указаны и точке х₀ односторонние пределы и значение функции в ней. Исследовать функцию на непрерывность в точке х₀ и устанавливать характер точки разрыва, если он есть:

а) f(x₀)=2, ;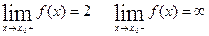

__________________________________________________________________

б) ;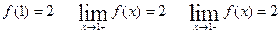

__________________________________________________________________

в) ;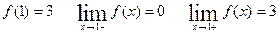

__________________________________________________________________

г)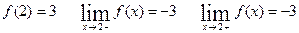

____________________________________________________________________________________________________________________________________

Задание 2. Выяснить, какие из функций непрерывны в точке х=2 (ответ обосновать);

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

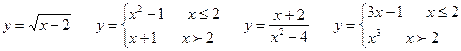
Задание 3. Исследовать функцию на непрерывность и найти точки разрыва функции (указать их характер):

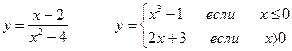
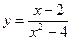
1. Находим область определения:

__________________________________________________________________

2. Рассмотрим поведение функции в точках_____________________________

а) х=__, найдём предел функции в ней _________________________________

_____________, значит х=___ точка разрыва _______________________рода;

б) х=__, найдём предел функции в ней _________________________________

значит х=__ точка _________________разрыва.

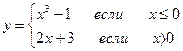
1. Находим область определения:

__________________________________________________________________2. Рассмотрим поведение функции в точках х=___,т. к. в ней функция изменяет своё поведение. Найдём односторонние пределы.

_______________________________,значит х=__ точка разрыва ____рода.

Date: 2015-04-23; view: 578; Нарушение авторских прав