
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема: Предел функции
|
|
1. Контрольные вопросы:
1. Что называется пределом функции в точке?
____________________________________________________________________________________________________________________________________
2. Что называется пределом функции на бесконечности?
____________________________________________________________________________________________________________________________________
3. Сформулируйте основные теоремы о пределах:
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4. Какая величина называется бесконечно малой? Приведите пример:
______________________________________________________________________________________________________________________________________________________________________________________________________
5. Какая величина называется бесконечно большой? Приведите пример:
______________________________________________________________________________________________________________________________________________________________________________________________________
6. Запишите первый и второй замечательные пределы.
__________________________________________________________________
2. Практические задания по теме:
Задание 1. Доказать, что число А является пределом функции:
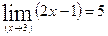 Возьмём любое e>0, составим неравенство |2x-1-5|<e, решим полученное неравенство |2х-6|<e «-e<2х-6<e «6-e<2х<6+e «
Возьмём любое e>0, составим неравенство |2x-1-5|<e, решим полученное неравенство |2х-6|<e «-e<2х-6<e «6-e<2х<6+e «
3-e/2<х<3+e/2 «|х-3|<e/2 «d=e/2
Итак, для любого e>0, нашли d=e/2, что для всех х, удовлетворяющих неравенству |х-3|<d, выполняется неравенство |2x-1-5|<e Þ 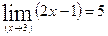 .
.
1. 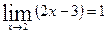
______________________________________________________________________________________________________________________________________________________________________________________________________
2. 
______________________________________________________________________________________________________________________________________________________________________________________________________
3. 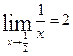
______________________________________________________________________________________________________________________________________________________________________________________________________
Задание 2. Найти предел функции:
При выполнении данного задания могут встретиться следующие неопределённости [ 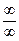 ], (
], ( ),(1µ). Чтобы устранить неопределённость 1-ого вида разделите числитель и знаменатель дроби на степень с наивысшим показателем, найти полученный предел см.(предел последовательности).
),(1µ). Чтобы устранить неопределённость 1-ого вида разделите числитель и знаменатель дроби на степень с наивысшим показателем, найти полученный предел см.(предел последовательности).
Чтобы устранить неопределённость 2-ого вида, можно разложить на множители и числитель, и знаменатель дроби или домножить и числитель, и знаменатель на одно и то же выражение, приводящее к формулам сокращенного умножения.
Рассмотрим ряд примеров:
Найти предел: 
| № | Алгоритмы | Выполнение соответствующего алгоритма |
| Подставить предельное значение х в выражение | ||
| Определить вид неопределённости | ||
| Разложить и числитель, и знаменатель дроби на множители | ||
| Сократить дробь | ||
| Подставить предельное значение х в сокращенную дробь |
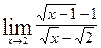
| № | Алгоритмы | Выполнение соответствующего алгоритма | |
| Подставить предельное значение х в выражение | |||
| Определить вид неопределённости | |||
| Умножим и числитель, и знаменатель дроби на сопряженные выражения | |||
| Выполнить преобразования | |||
| Подставить предельное значение х в сокращенную дробь |
Замечательные пределы:
1-ый замечательный предел: 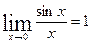
Найти пределы:1) 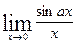 ; 2)
; 2)  ; 3)
; 3) 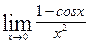 ; 4)
; 4) 
Решение: 1) Сделаем замену y=ax; тогда y®0 при х®0 и 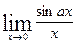 =
= 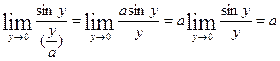
2) Поделим числитель и знаменатель дроби под знаком предела на х и воспользуемся предыдущим пределом:
 =
=  ;
;
3) Воспользуемся тригонометрическим тождеством: 1-cosx=2sin2  , тогда получим
, тогда получим
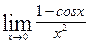 =
= 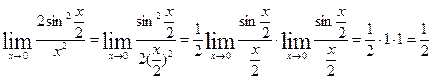
4) Сделаем замену y=arcsinx, тогда получим x=siny. Из того, что х®0, следует у®0, поэтому  =
=  .
.
2-ой замечательный предел: 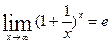 или
или 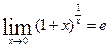
Найти пределы:1)  ; 2)
; 2) 
Решение:
1) В данном случае имеем неопределённость вида 1µ. Для её раскрытия воспользуемся 2-м замечательным пределом, сделав замену переменной 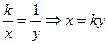 .Тогда у®µ при х®µ, выполним подстановку
.Тогда у®µ при х®µ, выполним подстановку  =
= 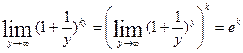
2) Для нахождения данного предела можно воспользоваться алгоритмом:
| № | Алгоритмы | Выполнение соответствующего алгоритма |
| Подставить предельное значение х в выражение | ||
| Определить вид неопределённости | ||
| Преобразовать выражение к виду, позволяющему использовать 2-ой замечательный предел |
Date: 2015-04-23; view: 850; Нарушение авторских прав