Простейшие статистические преобразования

Для обоснованных статистических выводов необходимо иметь выборку достаточно большого объема 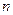. Очевидно, что использование и хранение такой выборки весьма затруднительно. Чтобы избавиться от данных проблем, используют понятие статистики.

Определение. Статистикой называется произвольная k‑мерная функция от выборки :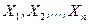

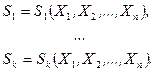
Как функция от случайного вектора статистика также будет случайным вектором.

Определение. Вариационным рядом 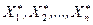является выборка 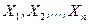, элементы которой расположены в порядке возрастания элементов: .

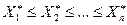Очевидно, что данное преобразование не приводит к потере информации относительно теоретической функции распределения.

Для величин 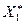и 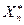употребляют название «крайние члены вариационного ряда».

Определение. Размахом варьирования называется разность между крайними членами вариационного ряда, т.е.

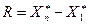. (7.2.1)

Если среди элементов выборки 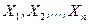имеются одинаковые, что происходит при наблюдении дискретной случайной величины, то целесообразно произвести группировку данных.

Определение. Значение выборки 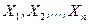, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантой, а численность отдельной группы сгруппированного ряда наблюдаемых данных, называется частотой или весом варианты.

Если 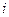— индекс варианты, то 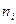— число значений 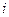‑ой варианты.

Определение. Отношение частоты 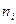к общей сумме всех частот называется относительной частотой варианты и обозначается .

Определение. Статистическим рядом называется расположенная по возрастанию совокупность различных вариант 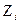, представляющих выборку 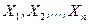, с соответствующими им частотами или относительными частотами.

При наблюдении непрерывной случайной величины используют интервальный ряд. В этом случае весь возможный интервал, которому принадлежат значения выборки, разбивают на конечное число частичных интервалов и подсчитывают частоту попадания элементов выборки в каждый частичный интервал.

Определение. Интервальным рядом называется упорядоченная последовательность интервалов с соответствующими им частотами или относительными частотами попадания элементов выборки в каждый из этих интервалов.

Пример 1. В городе A для определения сроков гарантированного обслуживания проведено исследование величины среднего пробега автомобилей, находящихся в эксплуатации в течение двух лет. Получены следующие результаты (тыс. км.):

3,0; 25,0; 18,6; 12,1; 10,6; 18,0; 17,3; 29,1; 20,0; 18,3; 21,5; 26,7; 12,2; 14,4; 7,3; 9,1; 2,9; 5,4; 40,1; 16,8; 11,2; 9,9; 25,3; 4,2; 29,6.

Составить интервальный ряд.

m Решение. Очевидно, что величина среднего пробега автомобилей, находящихся в эксплуатации в течение двух лет, является непрерывной случайной величиной. Полученные данные представляют собой выборку из 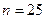наблюдений. Найдем сначала минимальное и максимальное значения случайной величины (т.е. крайние члены вариационного ряда): 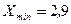и . Размах варьирования будет равен .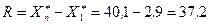

Возьмем число частичных интервалов 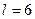. В этом случае длина частичного интервала равна

.

Соответствующий интервальный ряд приведен в таблице 7.1.

Таблица 7.1

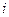
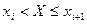
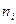
Номер интервала	Средний пробег автомобилей (интервалы)	Частота	Относительная частота
	2,9 — 9,1		0,24
	9,1 — 15,3		0,24
	15,3 — 21,5		0,28
	21,5 — 27,7		0,12
	27,7 — 33,9		0,08
	33,9 — 40,1		0,04

l

Пример 2. Наблюдается число выигрышей в мгновенной лотерее. В результате наблюдения получены следующие значения выигрышей (тыс. руб.):

0, 1, 0, 0, 5, 0, 10, 0, 1, 0, 0, 1, 5, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 5, 0, 5, 0, 0, 1, 1, 1, 5, 10, 0, 1, 1, 0, 5, 0, 0, 0, 0, 1, 0, 1, 0, 5, 0, 0, 0, 0, 1, 0.

Требуется составить статистический ряд случайной величины — выигрыша в мгновенной лотерее.

m Решение. Случайнаявеличина принимает 4 различных значения: 0, 1, 5 и 10. Для каждого значения подсчитаем частоту и относительную частоту.Результаты задачи представим в таблице 7.2.

Таблица 7.2

№
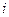
Выигрыш в мгновенной лотерее
Частота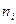
Относительная частота		31/54	7/27	7/54	1/27

l

Date: 2015-06-07; view: 1160; Нарушение авторских прав