Метод максимального правдоподобия

Метод максимального правдоподобия является наиболее распространенным методом нахождения оценок. Метод максимального правдоподобия опирается на использование условий экстремума функций одной или нескольких случайных величин. В качестве такой функции используется функция правдоподобия.

Определение. Функцией правдоподобия называется функция

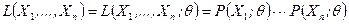(8.3.1)

в дискретном случае и

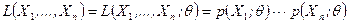(8.3.2)

в непрерывном случае.

В функции правдоподобия 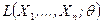элементы выборки 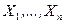являются фиксированными параметрами, а 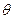— аргументом.

Определение. Оценкой максимального правдоподобия называется такое , для которого

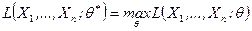. (8.3.3)

Поскольку 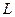и 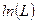принимают максимум при одном и том же значении аргумента 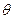, то при практической реализации метода максимального правдоподобия удобно использовать не саму функцию правдоподобия, а ее логарифм.

Определение. Уравнением правдоподобия называется уравнение

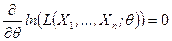. (8.3.4)

В случае, когда теоретическая функция распределения 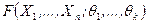зависит от нескольких параметров 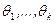, при применении метода максимального правдоподобия вместо уравнения (8.3.4) необходимо использовать систему уравнений

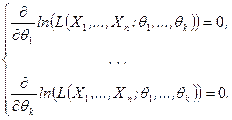(8.3.5)

Пример 4. Найти оценки параметров 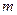(математическое ожидание) и 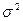(дисперсия) нормального закона распределения.

m Решение. Нормальный закон распределения характеризуется плотностью распределения

.

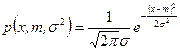Функция правдоподобия примет вид:

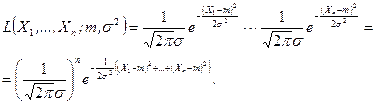(8.3.6)

Логарифмируя выражение (8.3.6), получим

. (8.3.7)

Подставляя (8.3.7) в систему (8.3.5), получим

(8.3.8)

Из первого уравнения системы (8.3.8) получаем

, (8.3.9)

а из второго уравнения системы (8.3.8), с учетом (8.3.9), получаем

.

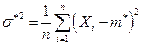Следует отметить, что полученная оценка является смещенной.

Читателю предлагается самостоятельно показать, что 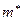и 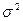доставляют максимум функции правдоподобия . l

Date: 2015-06-07; view: 526; Нарушение авторских прав