Метод моментов

Пусть имеется выборка 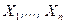, произведенная из генеральной совокупности с теоретической функцией распределения 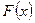, зависящей от параметров , которые нужно оценить. Зная функцию распределения, можно найти первые теоретических моментов, которые будут зависеть от параметров :

(8.2.1)

где — случайная величина, имеющая функцию распределения .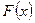

Метод моментов состоит в том, что в системе (8.2.1) при большом объёме выборки 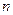теоретические моменты 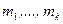заменяются на выборочные , а затем, решая эту систему относительно , находят оценки неизвестных параметров. Таким образом, в методе моментов оценки неизвестных параметров определяются из системы уравнений

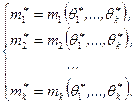(8.2.2)

Метод моментов был предложен в 1894 г. К. Пирсоном. Оценки, полученные методом моментов, как правило, являются состоятельными.

Пример 3. Выборка 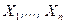произведена из генеральной совокупности с теоретической функцией распределения, имеющей плотность показательного закона

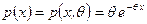
Найти оценку параметра .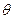

m Решение. Математическое ожидание случайной величины , имеющей плотность показательного закона, задаётся формулой

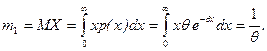
Используя систему (8.2.2), получаем .

Откуда окончательно получаем . l

Date: 2015-06-07; view: 532; Нарушение авторских прав