Математическое ожидание случайной величины

Определение. Математическим ожиданием 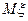дискретной случайной величины называется выражение, вычисляемое по формуле:

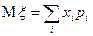, (6.1.1)

где 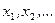— значения случайной величины, 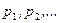— соответствующие им вероятности, которые определяются равенством .

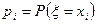Для существования математического ожидания необходимо, чтобы ряд (6.1.1) сходился абсолютно, т.е.

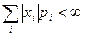, (6.1.2)

в противном случае говорят, что математическое ожидание не существует.

Пример 1. Пусть — случайная величина, равная числу выпавших очков при бросании игрального кубика. Найти математическое ожидание случайной величины .

m Решение. Случайная величина имеет следующий ряд распределения:

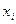
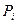
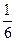
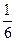
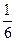
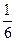
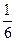
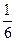
Применяя формулу (6.1.1), получим

.

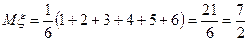Таким образом, математическое ожидание числа выпавших очков при бросании игрального кубика равно 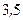. l

Пример 2. Найти математическое ожидание случайной величины — число успехов в схеме Бернулли.

m Решение. Как известно, распределение случайной величины задается формулой

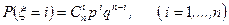
где 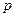— вероятность «успеха», 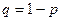, 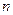— количество испытаний в схеме Бернулли.

Используя формулу (6.1.1), получим

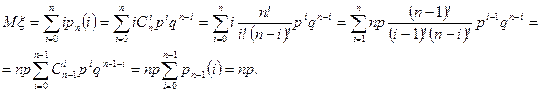
Таким образом, математическое ожидание числа успехов в схеме Бернулли равно 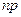. l

Определение. Математическим ожиданием 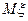непрерывной случайной величины называется интеграл:

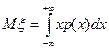. (6.1.3)

Условием существования математического ожидания непрерывной случайной величины является абсолютная сходимость интеграла

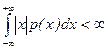. (6.1.4)

Пример 3. Найти математическое ожидание случайной величины , плотность которой имеет вид:

m Решение: Используя (6.1.3), получим

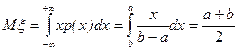. l

Пример 4. Найти математическое ожидание случайной величины , плотность которой имеет вид:

.

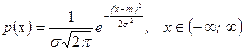m Решение. Используя (6.1.3), получим

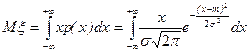. (6.1.5)

Делаем замену 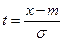или 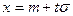. В этом случае (6.1.5) примет вид:

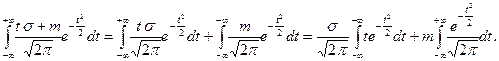(6.1.6)

Первое слагаемое равно нулю, т.к. равен нулю интеграл

.

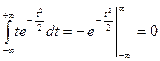Интеграл во втором слагаемом равен 1, т.к. этот интеграл равен функции распределения нормального закона с параметрами 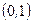при значении аргумента равным 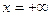, т.е.

.

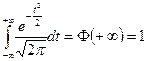Таким образом, математическое ожидание равно 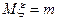. l

Пример 5. Случайная величина имеет плотность Коши:

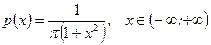. (6.1.7)

Проверить, имеет ли случайная величина математическое ожидание.

m Решение. Проверим условие (6.1.4) существования математического ожидания

.

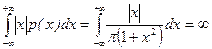Математическое ожидание случайной величины , имеющей плотность Коши, не существует, т.к. условие существования математического ожидания не выполнено. l

Date: 2015-06-07; view: 654; Нарушение авторских прав