Дискретные случайные величины

Как уже говорилось, дискретной называется случайная величина, которая каждому элементарному исходу 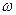ставит в соответствие одно из конечного (или в общем случае счетного) набора чисел .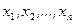

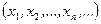Дискретную случайную величину удобно характеризовать рядом распределения.

Определение. Рядом распределения (вероятностей) дискретной случайной величины называется таблица (таблица 5.1), состоящая из двух строк: в первой строке перечислены все возможные значения случайной величины, а во второй — вероятности 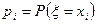того, что случайная величина примет значение .

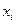Таблица 5.1

			…		…		…
			…		…		…

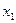
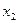
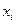
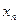
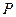
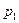
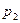
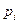
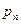
При этом должно выполняться равенство

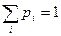. (5.3.1)

Функцию распределения дискретной случайной величины можно определить по формуле

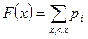. (5.3.2)

Пример 4. Производится один опыт, в результате которого может произойти событие 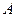с вероятностью 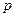. Рассмотрим случайную величину

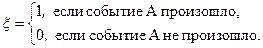
Для случайной величины ряд распределения и найти ее функцию распределения.

m Решение. Очевидно, что ряд распределения имеет вид:

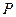
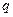
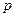
где .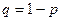

Функцию распределения случайной величины найдем по формуле (5.3.2).

Пусть 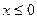. В этом случае событие 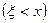является невозможным, так как случайная величина не принимает значений меньших 0. Отсюда получаем:

.

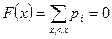Пусть 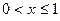. В этом случае событие 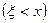совпадает с событием 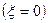, следовательно:

.

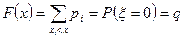Пусть 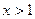. В этом случае событие 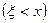является достоверным, следовательно

.

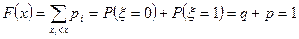Таким образом, функция распределения примет вид:

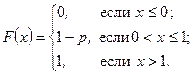
l

Пример 5. Рассмотрим схему последовательных независимых испытаний, в каждом из которых с вероятностью 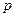может произойти событие 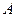. Рассмотрим случайную величину — число испытаний, которое необходимо произвести, прежде чем событие 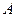произойдет. Построить ряд распределения случайной величины .

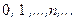m Решение. Случайная величина может принимать значения . Случайная величина принимает значение 0, если в первом же испытании произойдет событие 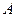, следовательно:

.

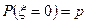Случайная величина принимает значение 1, если в первом испытании событие 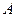не произошло, а во втором испытании событие 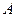произойдет, следовательно,

.

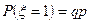Случайная величина принимает значение 2, если в первых двух испытаниях событие 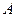не произошло, а в третьем испытании событие 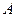произойдет, следовательно,

.

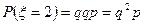Продолжая аналогично данные рассуждения, получим ряд распределения:

				…		…
				…		…

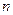
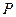
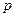
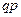
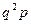
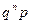
l

Пример 6. На зачете студент получил 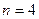задачи. Вероятность решить правильно каждую задачу 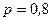. Построить ряд распределения случайной величины — числа правильно решенных задач.

m Решение. Случайная величина может принимать значения 0, 1, 2, 3, 4. Для нахождения вероятности событий 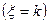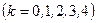применим формулу Бернулли:

,

,

,

,

.

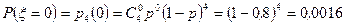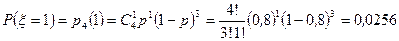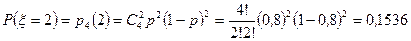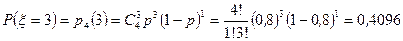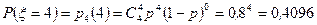Таким образом, ряд распределения числа правильно решенных задач примет вид:

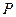
	0,0016	0,0256	0,1536	0,4096	0,4096

l

Date: 2015-06-07; view: 503; Нарушение авторских прав