Свойства функции распределения

1. Функция распределения является ограниченной, т.е.

.

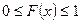Доказательство. Ограниченность функции распределения следует из того, что функция распределения является вероятностью. n

2. Функция распределения является неубывающей, т.е. если 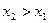, то

.

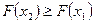Доказательство. Если 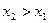, то событие 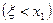содержится в событии 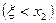, т.е. 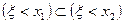. Отсюда, по свойству 3 вероятности, имеем

,

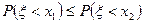откуда, следует

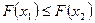. n

3. 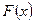обращается в ноль на минус бесконечности, т.е.

.

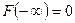Доказательство. Событие является невозможным событием, следовательно, 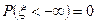. n

4. 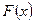равна единице в плюс бесконечности, т.е.

.

Доказательство. Событие 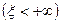является достоверным событием, следовательно, .

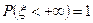5. Вероятность попадания случайной величины в интервал равна приращению ее функции распределения на этом промежутке, т.е.

.

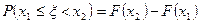Доказательство. При 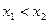событие 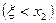можно представить как объединение двух непересекающихся событи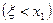й и 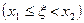. Отсюда, используя аксиому сложения, получаем

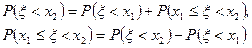
или, используя определение функции распределения, получаем

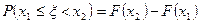. n

6. 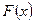непрерывна слева, т.е.

.

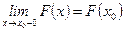С помощью функции распределения можно вычислить вероятность события :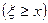

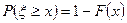.(5.2.2)

Иногда, чтобы подчеркнуть, кокой именно случайной величине принадлежит функция распределения 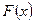, к функции распределения приписывают нижний индекс, обозначающий эту случайную величину, т.е.

.

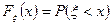Иногда функцией распределения называется вероятность события 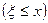. Такое определение ничего не меняет во всех рассуждениях. Единственное изменение касается свойства 6: функция 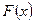будет непрерывной справа.

Date: 2015-06-07; view: 563; Нарушение авторских прав