Формула Пуассона

При больших значениях числа испытаний 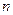применение формулы Бернулли (4.1.2) затруднительно. Поэтому применяются простые, но достаточно точные приближенные формулы для вычисления 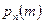. Пусть число испытаний 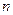достаточно «велико», вероятность «успеха» 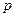достаточно «мала». Пусть произведение

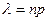(4.2.1)

и не мало, и не велико. В таких случаях удобно использовать для вероятности 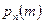предложенное Пуассоном приближение (формула Пуассона), которое мы сейчас выведем. По формуле Бернулли (4.1.2)

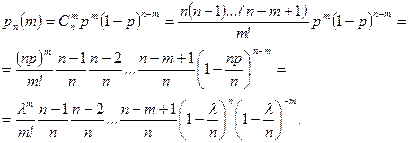(4.2.2)

При 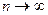и сделанных выше допущениях очевидны следующие приближения:

, .

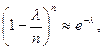
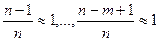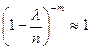Следовательно, (4.2.2) примет вид:

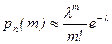, (4.2.3)

а это и есть формула Пуассона.

Замечание. При выводе формулы Пуассона (4.2.3) использовалось то, чт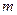о мало.

Замечание. Формула Пуассона (4.2.3) зависит от 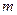и . Значения функции (4.2.2) можно определить следующими способами:

§ можно воспользоваться Приложением 1;

§ используя функцию ПУАССОН (x;среднее;интегральная) из EXCEL; в которой аргумент x равен числу «успехов» 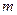, аргумент «среднее» равен , аргумент «интегральная» должен равняться 0;

§ используя функцию dpois(k, l) из MATHCAD, в которо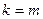й и .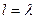

Пример 4. Найти вероятность того, что среди 1460 человек ровно трое родились 29 февраля.

m Решение. Вероятность того, что один конкретный человек родился 29 февраля, равна 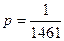, т.к. 29 февраля бывает ровно 1 раз в 4 года.

Далее находим коэффициент :

.

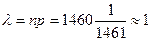Применяя (4.2.2), получаем:

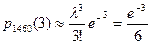. l

Пример 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность того, что при 5000 выстрелах в цель попало не менее двух выстрелов.

m Решение. Рассмотрим два противоположных события:

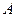— при 5000 выстрелах в цель попало не менее двух выстрелов;

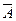— при 5000 выстрелах в цель попало менее двух выстрелов.

Найдем вероятность события :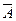

.

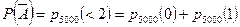В рассматриваемом примере

.

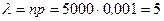Используя формулу Пуассона, получим

.

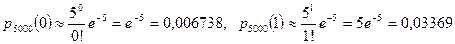Используя свойство вероятности противоположного события, получим

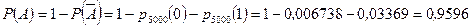. l

Date: 2015-06-07; view: 2327; Нарушение авторских прав