Элементы треугольной формы

Если исходная пластина имеет произвольную границу, то форма КЭ в виде треугольника позволяет с высокой степенью точности представить область W как совокупность конечных элементов. Выбирая вершины треугольника в качестве узловых точек, получаем, что число степеней свободы такого КЭ равно 9. Наиболее подходящий полином для описания изгиба пластины имеет третий порядок:

.

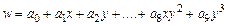Но число параметров, определяющих этот полином, превосходит число 9. Для выполнения равенства числа степеней свободы КЭ и количества параметров интерполирующего полинома введем еще одну узловую точку. Принято в качестве такой точки выбирать центр тяжести треугольника – внутреннюю точку КЭ, которая не совпадает ни с одним узлом других элементов. Если приписать узлу 4 лишь одну степень свободы, например, перемещение по оси 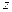, то между параметрами 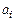и степенями свободы КЭ можно установить взаимно однозначное соответствие и тем самым получить решение задачи интерполяции перемеще-ний для точек КЭ. Выберем произвольный конечный элемент
с номером .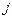

На рис. 4.10 показаны локальные номера узлов этого элемента. Свойства КЭ удобно определить в локальной системе координат, которая вводится таком способом: начало осей располагается в узле 1 КЭ, ось x совпадает с узлом 2, а ось h направлена в сторону узла 3. Направление оси z выбирается так, чтобы локальная система координат была правой. Заметим, что в нашем случае направления осей z и z совпадают, так как движение от узла 1 к 2 и 3 является обходом границы КЭ против часовой стрелки.

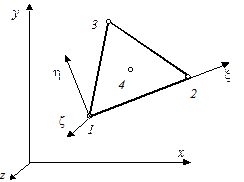
Рис. 4.10. Треугольный КЭ изгибаемой плас-

тины и локальная система координат

Установим связь между глобальными и локальными системами координат. Пусть 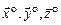– орты глобальной системы. Вычислим орты локальных осей. Из простых геометрических соотношений имеем:

.

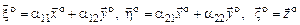Здесь введены обозначения:

.

Отметим, что значение перемещения по нормали к поверхности пластины в разных системах координат одно и то же. Обозначим через 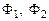– проекции вектора, определяющего углы поворота точек срединной поверхности пластинки на локальные оси. Тогда перемещения и углы поворота в глобальных и локальных осях связаны между собой формулой:

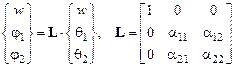. (4.30)

Обозначим через 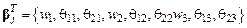вектор-столбец перемещений и углов поворота узловых точек в глобальной системе координат. Для вычисления матрицы жесткости КЭ в локальной системе координат определим еще один век-
тор-столбец:

.

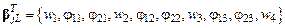Здесь 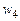– перемещение точки КЭ, расположенной в центре тяжести треугольника. Перемещение точек срединной поверхности зададим с помощью полинома третьего порядка в виде произведения векторов:

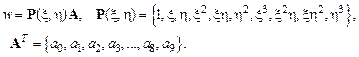
Параметры 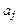найдем, вычисляя прогибы и углы поворота узловых точек:

.

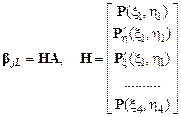Решение этой системы уравнений имеет вид:

.

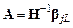Произведение 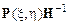является вектором-строкой десятого порядка, элементы которой представляют собой функции формы 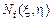для рассматриваемого конечного элемента.
Поэтому они определены выражением:

.

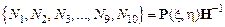Теперь интерполирующий полином зависит только от перемещений и углов поворота узловых точек, определенных в локальной системе координат:

.

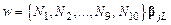Определим векторы и :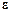

.

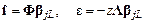Здесь введены обозначения:

.

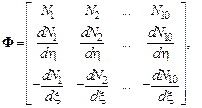
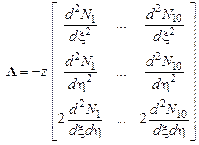Вычисление разности работ внутренних и поверхностных сил приводит к такому результату:

.

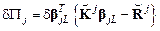В этой формуле 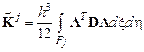– матрица жесткости элемента, 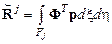– вектор-столбец узловых нагрузок. Заметим, что эти объекты вычислены в локальной системе координат и, в отличие от разности работ dP _j, зависят от ее ориентации. Выполним преобразование dP _j путем исключения из матрицы жесткости перемещения внутреннего узла 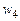и пересчета данных в глобальной системе координат. Для этого преобразуем вектор-столбец перемещений, заданный в локальной системе координат, к виду:

.

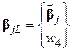Отметим, что введенный вектор не содержит перемещения узла 4:

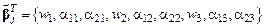. (4.31)

Представим в такой же форме и возможные перемещения узлов конечного элемента:

.

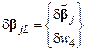Теперь сформируем матрицу жесткости конечного элемента и узловые нагрузки в виде блоков, соответствующих структуре вектора перемещений 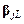. Выпишем эти объекты, не указывая связанный с ними номер конечного элемента:

.

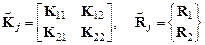Заметим, что величины 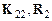являются обычными числами (скаляры). Теперь в выражении работы внутренних сил выделим отдельно слагаемые, обусловленные возможным перемещением узла 4:

.

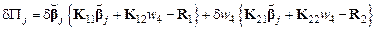Так как приращение работы для всей пластины равно нулю, то из независимости второго слагаемого от возможных перемещений и углов поворота других узлов следует:

.

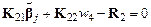Это уравнение определяет 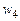, что позволяет преобразовать работу внутренних сил путем исключения перемещения узла 4:

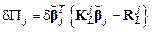. (4.32)

Здесь введены обозначения новой матрицы жесткости и вектора-столбца узловых нагрузок, определенных для вектора (5.6):

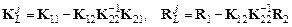. (4.33)

Для формирования матрицы жесткости и вектора-столбца узловых нагрузок для всей пластины следует пересчитать объекты (4.33) в глобальной системе координат. Это выполняется с помощью матрицы 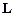, приведенной в (4.30). Образуем матрицу девятого порядка из диагональных блоков :

.

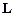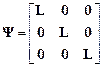Векторы-столбцы перемещений в глобальных и локальных осях связаны соотношением:

.

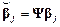Подставляя в выражение работ на возможных перемещениях формулу (4.32), получим:

.

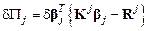Здесь введены обозначения 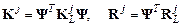. Дальнейшее формирование матрицы 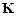и вектора 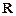для всей пластины выполняется стандартным образом.

Date: 2015-06-07; view: 521; Нарушение авторских прав