Полная энергия пластины

В соответствии с принятыми выше допущениями, слои, параллельные срединной поверхности, находятся в условиях плоского напряженного состояния. Поэтому соотношения упругости для любой точки пластинки можно представить в виде:

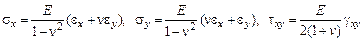. (4.28)

Как следует из соотношений (4.27), напряжения зависят от координаты 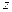. Поэтому для вычисления потенциальной энергии пластинки вырежем в бесконечно малом элементе 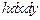слой толщины 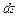. Так как слой испытывает плоское напряженное состояние, усилия в слое определены формулами:

.

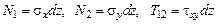Подставляя эти усилия в подынтегральное выражение (4.8), получим для энергии слоя:

.

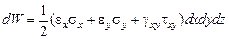Интеграл по всему объему пластинки приводит к такому значению потенциальной энергии пластинки:

.

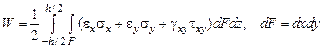Вычислим работу внешних поверхностных сил, действующих на рассматриваемый элемент. Из принципа «замораживания» внешних сил имеем:

.

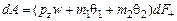Аналогично предыдущим вычислениям имеем:

.

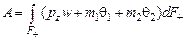Таким образом, полная энергия пластинки определяется формулой:

.

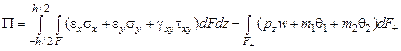Преобразуем это выражение для упрощения дальнейших вычислений. Введем обозначения:

.

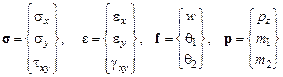Представим закон Гука (4.28) в такой форме:

.

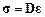Здесь 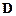– матрица упругих параметров, описывающих свойства материала:

.

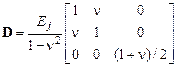Окончательно имеем представление полной энергии в виде:

.

Анализ вывода уравнений равновесия (4.25) приводит к заключению: представляет интерес вычисление не полной энергии пластинки, а лишь ее приращения на перемещениях 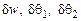. Тогда имеет смысл сразу вычислять приращение полной энергии для всей пластинки. Изменение перемещений вызывает приращение относительных деформаций 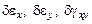. Представим эти приращения в векторной форме:

.

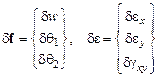Теперь вычислим приращение полной энергии пластинки 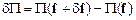. С точностью до величин первого порядка малости имеем:

.

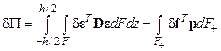Отметим, что нагрузку, действующую на поверхность 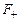, можно перенести на срединную поверхность 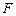с сохранением условий статической эквивалентности. Тогда полученную формулу заменим следующей:

.

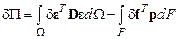Преимущество этой записи заключается в том, что вычисление интегралов выполняется по одной и той же поверхности, так как .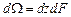

Date: 2015-06-07; view: 450; Нарушение авторских прав