Прямоугольные конечные элементы

Задача вычисления матрицы жесткости 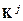и вектора 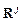наиболее просто решается для прямоугольного четырехузлового конечного элемента. Для иллюстрации расчетов остановимся на случае, когда 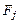представляет собой квадрат со стороной, равной единице, и КЭ расположен в начале системы координат (рис. 4.9). Занумеруем узлы конечного элемента. Примем, что каждый узел имеет три степени свободы перемещений и поворотов. Тогда деформированное состояние КЭ определяется следующими двенад-цатью параметрами 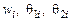. Здесь 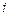принимает значения номеров узлов от 1 до 4. 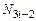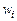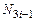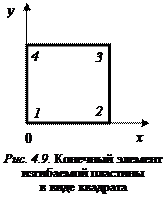Введем следующие обозначения функций формы КЭ: – для перемещений узлов ; – для углов 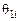; 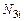– для углов 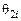. Отметим свойства этих функций. Например, 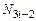принимает значение 1 в узле 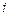и 0 – в остальных; кроме этого, первые производные функций 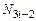по переменным 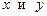во всех узлах равны нулю; 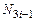и ее производные принимают нулевое значение в узлах КЭ, за исключением производной по координате 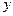в узле 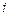, которая равна единице. Для функции 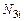лишь производная по переменной 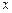в узле 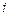равна единице. Конкретное представление функций формы для квадрата получим с помощью полиномов Лагранжа первого порядка:

,

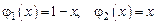и интерполяционных формул Эрмита с использованием полиномов третьей степени:

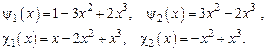
Эти функции удовлетворяют однородным уравнениям растяжения и изгиба упругой балки и широко используются в расчетах стержневых систем. Образуем такие полиномы:

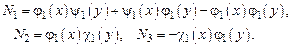
Непосредственная проверка показывает, что эти функции удовлетворяют всем перечисленным выше требованиям и являются функциями формы для узла 1. На их основе можно сконструировать соответствующие функции и для других узлов. Например, для узла 2 имеем:

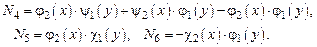
Остальные полиномы не будем приводить из-за очевидной их структуры. Задача интерполяции перемещений и углов поворота

для точек конечного элемента решается как суперпозиция построенных функций:

.

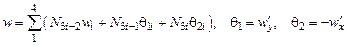Векторы-столбцы перемещений и деформаций представим в удобной форме:

,

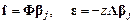где введены обозначения:

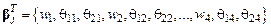, (4.29)

.

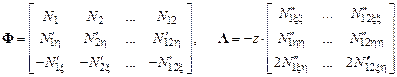Приращения перемещений 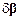и обусловленные ими относительные деформации d e определим так же, как и ранее, используя введенные функции формы:

.

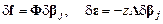Вычисление разности работ внутренних и поверхностных сил приводит к такому результату:

.

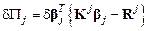В этой формуле 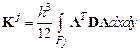– матрица жесткости конечного элемента; 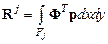– вектор-столбец узловых нагрузок.

Необходимо отметить, что применение КЭ в виде прямоугольников возможно лишь в случае, когда граница срединной поверхности s является ломаной, образованной из прямолинейных взаимно перпендикулярных отрезков. Для применения полученных здесь результатов следует для каждого КЭ вводить локальные системы координат с обязательным преобразованием вычисленных матриц жесткости и узловых нагрузок в глобальной системе координат. Далее подобные преобразования рассмотрим детальнее.

Date: 2015-06-07; view: 567; Нарушение авторских прав