Вычисление полной энергии КЭ

Разделение пластины на КЭ должно удовлетворять двум тождествам:

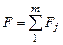и 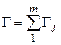. (4.11)

Однако если КЭ не примыкает к границе области 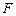, то для таких КЭ граница Г _j может быть вырожденной. Из тождеств (4.11) следует, что полная энергия пластины может быть представлена суммой по всем КЭ:

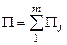. (4.12)

Здесь введено обозначение:

.

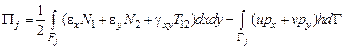Отметим, что степени свободы деформирования j -го КЭ – это перемещения узловых точек. Из таблицы КЭ имеем номера этих узлов 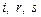. Образуем из перемещений узлов КЭ вектор-столбец шестого порядка:

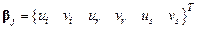. (4.13)

Основная задача состоит в том, чтобы с помощью набора подходящих функций выразить через компоненты вектора 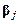перемещения любой точки КЭ и относительные деформации. Решение задачи интерполяции перемещений 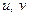должно быть однозначным и допускать перемещение КЭ как абсолютно жесткого тела. Этим условиям в данном случае удовлетворяет линейный закон изменения перемещений:

.

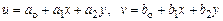В узловых точках значения 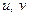совпадают с перемещениями узлов 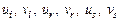. Таким образом, имеем шесть уравнений для определения постоянных a ₀, a ₁, a ₂, b ₀, b ₁, b ₂. Решение уравнений представим в удобной для дальнейших вычислений форме:

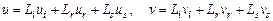. (4.14)

Здесь 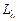– линейные полиномы от 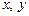, зависящие от координат узлов КЭ и удовлетворяющие условиям:

.

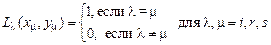Полиномы L _l, обладающие такими свойствами, принято называть функциями формы перемещений конечного элемента. После определения постоянных a ₀, a ₁, а ₂, b ₀, b ₁, b ₂ и приведения к виду (4.14) получаем следующие представления для функций формы L _l:

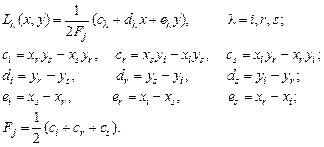
По найденным перемещениям вычислим относительные деформации по формулам (4.3) и (4.4):

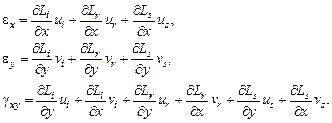(4.15)

Вычисление полной энергии КЭ по формуле (4.12) приводит, после весьма громоздких вычислений, к квадратичной форме относительно перемещений узловых точек. Этот же результат можно получить в более наглядной форме, удобной и для составления равновесия узлов всей пластины.

Введем векторы-столбцы:

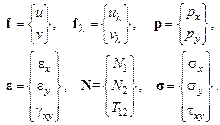(4.16)

Здесь f _l – вектор-столбец перемещений узла с номером l. Преимущества такой записи параметров становятся понятными, если использовать операции произведения векторов и матриц. Например, 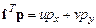. Отметим также простую связь между напряжениями и внутренними силами: 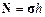. Теперь запишем выражение полной энергии КЭ в виде:

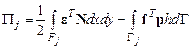. (4.17)

Векторам, входящим в выражение энергии, следовало бы приписать индекс j, указывающий на номер конечного элемента. Чтобы не загромождать формулы, условимся не задавать такие индексы.

Выразим объекты 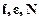через вектор-столбец перемещений узлов КЭ. Из формул (4.15), (4.16) и (4.5) следует:

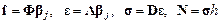. (4.18)

Здесь введены обозначения:

,

.

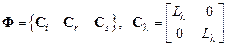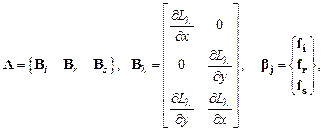
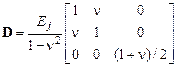Заметим, что компоненты вектора 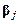не зависят от переменных интегрирования, поэтому вектор можно выносить из интегралов по поверхности и границе области пластины:

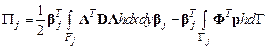. (4.19)

Интегралы, входящие в выражение полной энергии, содер-жат матрицу жесткости 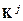и вектор-столбец узловых нагрузок 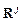j -го КЭ:

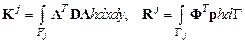. (4.20)

Эти объекты позволяют записать полную энергию КЭ (4.19) в такой форме:

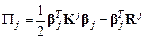. (4.21)

Заметим, что матрицы и векторы, входящие в правую часть квадратичной формы (4.21), имеют блочную структуру (4.18):

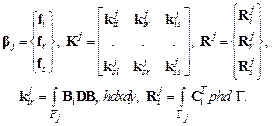
Это свойство дает возможность преобразовать выражение полной энергии (4.21) к виду:

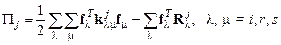. (4.22)

Date: 2015-06-07; view: 453; Нарушение авторских прав