Уравнения равновесия пластины

Полная энергия пластины 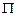образована суммой (4.12). Из анализа формулы (4.22) следует, что квадратичная форма 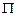имеет такую же структуру:

,

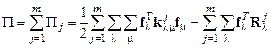где 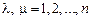для всех КЭ.

Переставляя операции суммирования и вводя обозначения

,

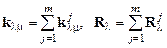получим

.

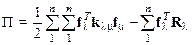Отметим, что суммирование ведется по всем элементам, примыкающим к узлам с одинаковыми номерами .

Для вывода уравнений равновесия введем векторы и матрицы для всей пластины:

.

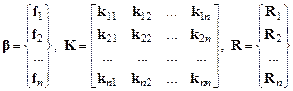Эти величины дают возможность записать полную энергию в таком виде:

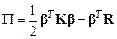. (4.23)

Вычислим изменение полной энергии, обусловленное приращением вектора перемещений 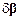. Вычисления, аналогичные выполненным в предыдущих разделах, приводят к результату:

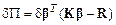. (4.24)

Если 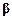соответствует минимуму значения 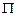, то необходимо выполнение условия:

.

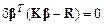Полагая, что компоненты вектора 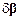являются линейно независимыми бесконечно малыми величинами, получаем уравнения равновесия узлов пластины:

. (4.25)

Подчиняя (4.25) граничным условиям и решая полученную систему уравнений, находим перемещения узловых точек всей пластины. Далее по формулам (4.18) вычисляем относительные деформации и внутренние силы в элементах пластины.

Date: 2015-06-07; view: 502; Нарушение авторских прав