Основные допущения теории изгиба пластин

Если пластинку рассматриваем как трехмерное тело, то приходим к решению трехмерной задачи теории упругости. Но желание упростить расчет – считать, что перемещения точек срединной поверхности однозначно определяют деформированное и напряженное состояния рассматриваемого тела – приводит к необходимости ввода ряда допущений. В теории изгиба пластин используются следующие гипотезы.

· Слои пластины, параллельные срединной поверхности, не надавливают друг на друга. Это утверждение эквивалентно условию , которое упрощает задачу вычисления напряжений в теле пластины. Кроме того, это допущение позволяет считать, что тонкие слои пластинки испытывают плоское напряженное состояние.

· Точки пластины, расположенные на нормали к срединной поверхности, в процессе приложения нагрузки остаются расположенными на нормали к деформированной срединной поверхности. Это допущение принято называть гипотезой Кирхгофа или гипотезой прямых нормалей.

· Перемещения точек срединной поверхности малы по сравнению с толщиной пластины. Из этого положения следует, что малы и углы поворота сечений пластины: .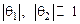

Date: 2015-06-07; view: 559; Нарушение авторских прав