Алгоритмы ветвящейся структуры

Часто в зависимости от каких-либо значений промежуточных результатов необходимо организовать вычисление либо по одним, либо по другим формулам, т. е. в зависимости от результата выполнения некоторого логического условия вычислительный процесс должен идти по одной или другой ветви. Алгоритм такого вычислительного процесса называется алгоритмом ветвящейся структуры. В общем случае количество ветвей в таком алгоритме не обязательно равно двум.

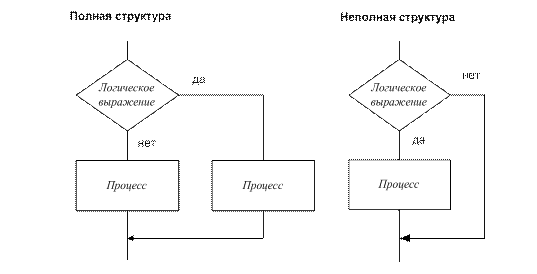
Рис. 19.

Пример 3. Составить схему алгоритма вычисления значения функций А (рис. 20):

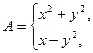
Требуется вычислить значение A либо по одной, либо по другой формуле, в зависимости от значения x >3 или x ≤3.

В блоке 1 осуществлен ввод переменных x и y. Блок 2 осуществляет ветвление вычислительного процесса. Внутри блока записывается условие. Из такого блока два выхода: один на ответ «да», другой - на ответ «нет». При ответе «да» на условие «x >3» следует А присвоить значение х ²+ у², а при ответе «нет» А присвоить значение х - у ². После вычисления требуется осуществить вывод значения А, что и делаем в блоке 4. Таким образом, в зависимости от введенной переменной x (у может иметь любое значение) ход вычислительного процесса будет идти или по блокам 1, 2, 5, 4 (если x >3), или по блокам 1, 2, 3, 4 (если x≤3).

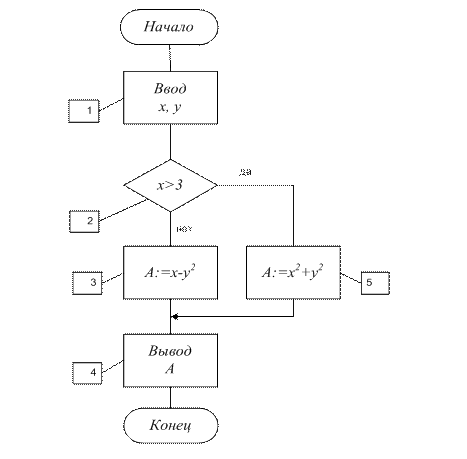
Рис. 20.

Пример 4. Составить схему алгоритма вычисления функции у (рис. 21):

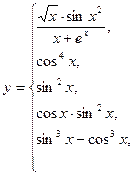
Ставится задача вычисления значения у по одной из пяти формул в зависимости от значения переменной х.

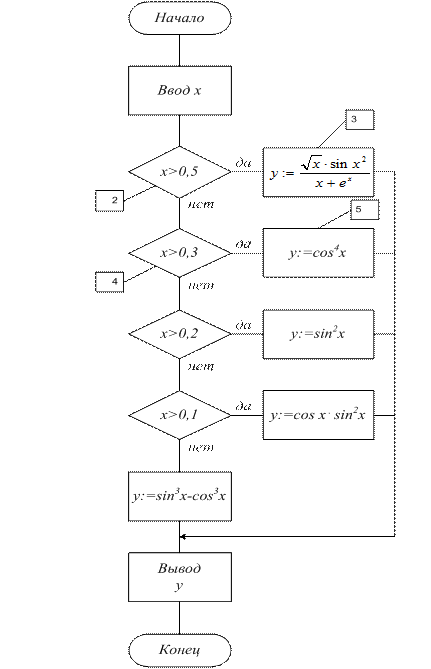
Рис. 21.

На выходе из блока 2 по ответу «да» имеем значение x >0,5 и в блоке 3 вычисляем y.

На выходе из блока 2 по ответу «нет» имеем значения x ≤0,5 и в блоке 4 отбираем значения x >0,3. Записывать в блоке 4 условие 0,3< x ≤0,5 не стоит, так как на входе в блок 4 уже имеем значения x ≤5 (либо двойное условие записывают через логические связки – «и», «или»). При выходе из блока 4 на ответ «да» получаем значения 0,3<x≤0,5 и вычисляем у в блоке 5, а на ответ «нет» значение x ≤З.

Дальнейший ход рассуждений аналогичен приведённому. Необходимо обратить внимание на то, что при ветвлении на n веток при построении алгоритма имеем n -1 логических блоков. Ветвящийся алгоритм можно создавать в соответствии с поставленной задачей и структурой программы, где количество блоков «решение» будет соответствовать количеству структурных логических операторов в программе.

Пример 5. Составить схему алгоритма вычисления величины y по заданному значению аргумента x (рис. 23).Функция y = f (x) задана графически (рис. 22):

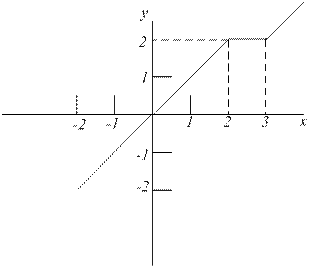
Рис. 22.

Как видно на графике, для значений аргумента x<2 функция задана прямой, пересекающей ось x под углом 45° в точке x = 0, а для нее уравнение имеет вид у = х. На отрезке 2≤x<3 график функции параллелен оси x, т. е. для этих значений аргументов у = 2. Для значения x≥3 график функции снова представляет собой прямую под углом 45°, и аналитическая зависимость: y = x – 1.

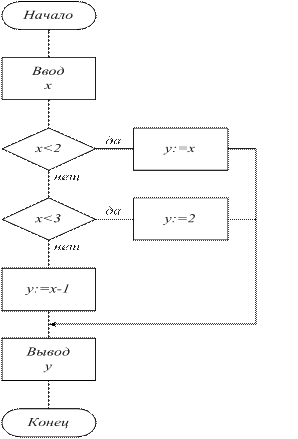
Рис. 23.

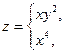
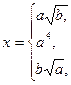
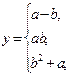
В зависимости от введенных значений а и b значение х будет вычислено по одной из трех формул к точке входа в блок 7. К точке входа в блок 12 будут вычислены х и у. В блоках 13 или 14 будет вычислена величина z, в зависимости от соотношения вычисленных в предыдущих блоках величин х и у.

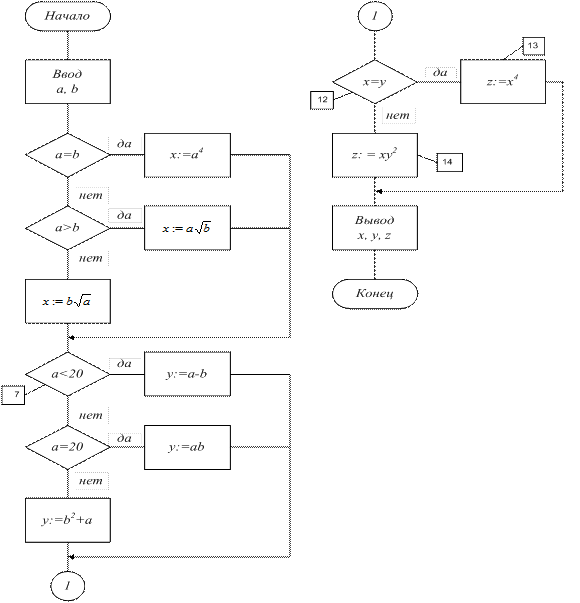
Рис. 24.

Пример 7. Составить схему алгоритма нахождения максимального числа среди трех элементов (рис. 25):

M =max(a,b,c).

Приведены два варианта составления алгоритма поставленной задачи (рис.25, 26).

В первом варианте (рис. 25, а) в блоке 2 сравнивают две переменные а и b, и в зависимости от того, какая величина больше, искомой переменной М присваивают значение наибольшего из а и b. Таким образом, к блоку 5 переменная М будет иметь значение наибольшего из двух чисел a и b. В блоке 5 полученное значение М сравниваем с третьей переменной с, и в зависимости от того, больше ли М переменной с или нет, оставляем старое значение М или присваиваем ей значение переменной с. В блоке 7 выводим полученное значение М, которое равно наибольшему из трёх переменных. Второй вариант (рис. 25, б) более длинный и громоздкий.

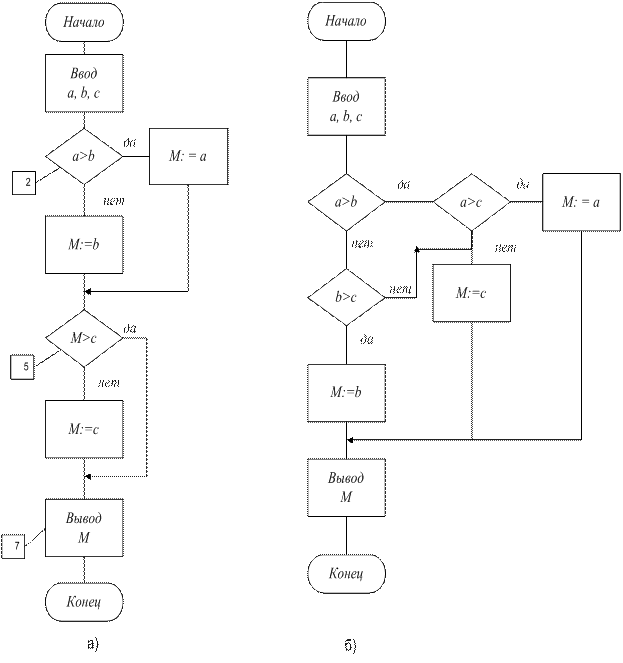
Рис. 25.

Аналогичные схемы будут и при вычислении максимального (минимального) значения для четырех величин, но во втором варианте это крайне усложнит алгоритм. Для обработки большого количества переменных из них создают массив, который обрабатывается циклическим процессом.

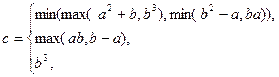
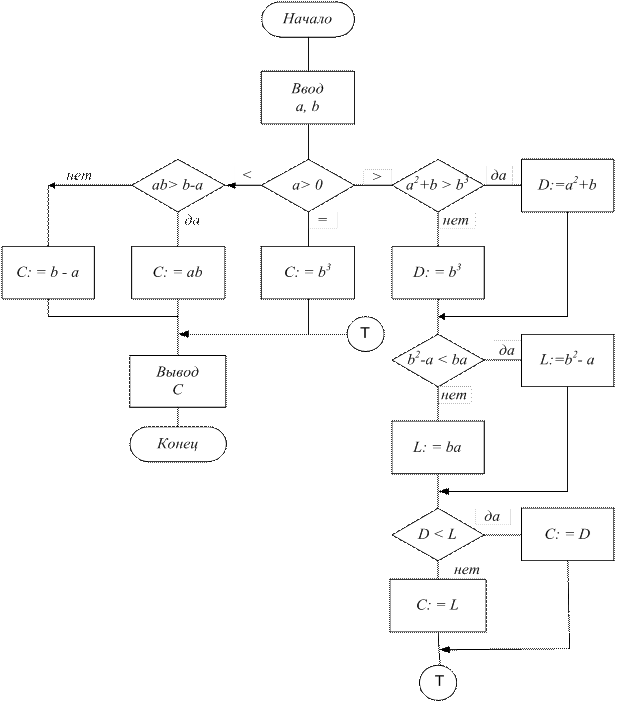
Рис. 26.

Date: 2015-06-06; view: 1520; Нарушение авторских прав