Циклы с неизвестным числом повторений (итерационные)

Пример 13. Составить схему алгоритма для определения количества чисел натурального ряда, которые надо сложить, чтобы получить сумму, большую 5000

(рис. 31, приведён вариант цикла с постусловием).

В данной задаче не известно сколько раз осуществится прохождение цикла, и проверка на окончание цикла (блок 4) будет по получаемой сумме S. В алгоритме итерационного цикла все те же составляющие, что и в арифметическом цикле. Блоки 1, 2 — подготовка цикла; блок 3 — тело цикла; блок 4 — блок модификации; блок 5 —проверка завершения цикла.

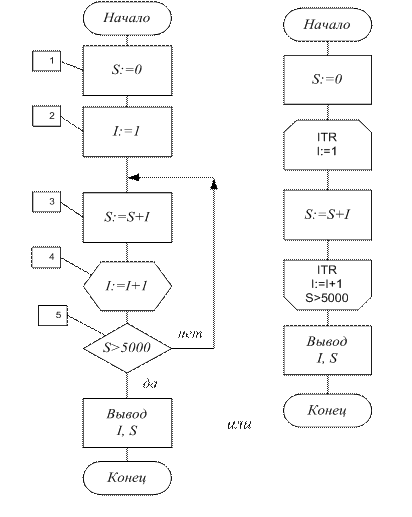
Рис. 31.

Пример 14. Составить схему алгоритма для приближённого вычисления суммы бесконечного ряда:

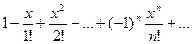
Суммирование производить до тех пор, пока очередное слагаемое не станет по абсолютной величине меньше заданного числа (рис. 32, приведён вариант цикла с предусловием).

Если обозначить слагаемые суммы через 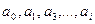, то можно написать следующие соотношения:

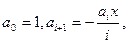где i = 1, 2, 3,…

Новое значение слагаемого получаем, пользуясь рекуррентной формулой. Цикл заканчиваем, как только очередное слагаемое будет по абсолютной величине меньше введенного ε (блок 5).

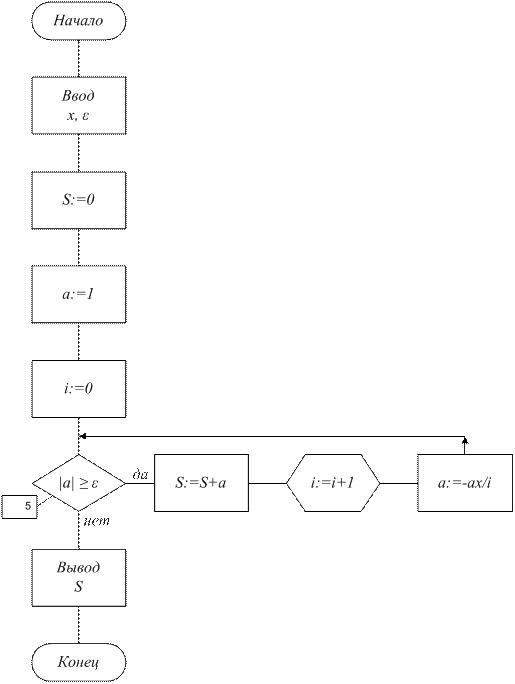
Рис. 32.

Date: 2015-06-06; view: 747; Нарушение авторских прав