Массивы

Одним из фундаментальных понятий в программировании является понятие массива. В программировании массивом называется поименованная совокупность элементов с одинаковыми свойствами. Для обозначения этой совокупности используются имя и размерность. Размерность отражает внутреннюю структуру массива, т. е. взаимное расположение элементов по отношению друг к другу. Массивы могут быть одномерными (вектора), двумерными (матрицы), трехмерными, n-мерными.

Элементы массива располагаются в памяти ЭВМ в последовательных ячейках (нумерация или индексация ячеек начинается с нуля, нулевую ячейку можно не использовать при заполнении массива). Для обозначения элементов массива используются индексированные переменные. В зависимости от размерности это переменные с одним, двумя, тремя индексами. Например: A(I) или A[I] — элемент одномерного массива, где A – имя массива, I – индекс (номер) ячейки массива; B(I, J) или B[I, J] – элемент двумерного массива, где B – имя массива, I - индекс (номер) строки массива, J – индекс (номер) столбца массива. Двумерные массивы могут быть квадратичной формы – квадратные матрицы, если количество строк равно количеству столбцов. В квадратной матрице индексы элементов: на главной диагонали равны (I=J), над главной диагональю I<J, под главной диагональю I>J.

Например: в одномерном массиве A(8) находится девять элементов: A(0), А(1), А(2), А(3),…, А(8) (рис. 33).

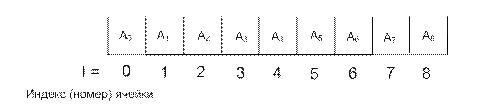
Рис. 33.

Например: в двумерном массиве С(5, 4), имеющем 5 строк и 4 столбца находится двадцать элементов, если не заполнять нулевые строку и столбец: С(1, 1), С(1, 2), С(1, 3), С(1, 4), С(2, 1)),…,С(5, 4) (рис. 34).

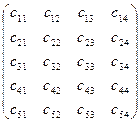↓I – индекс (номер) строки

→

J – индекс (номер) столбца

Рис. 34.

То обстоятельство, что массив имеет одно имя и элементы массива отличаются индексами (номерами ячеек), позволяет обрабатывать их в цикле, изменяя значения индексов.

Пример 15. Составить схему алгоритма вычисления суммы элементов одномерного массива A (30) (рис. 35).

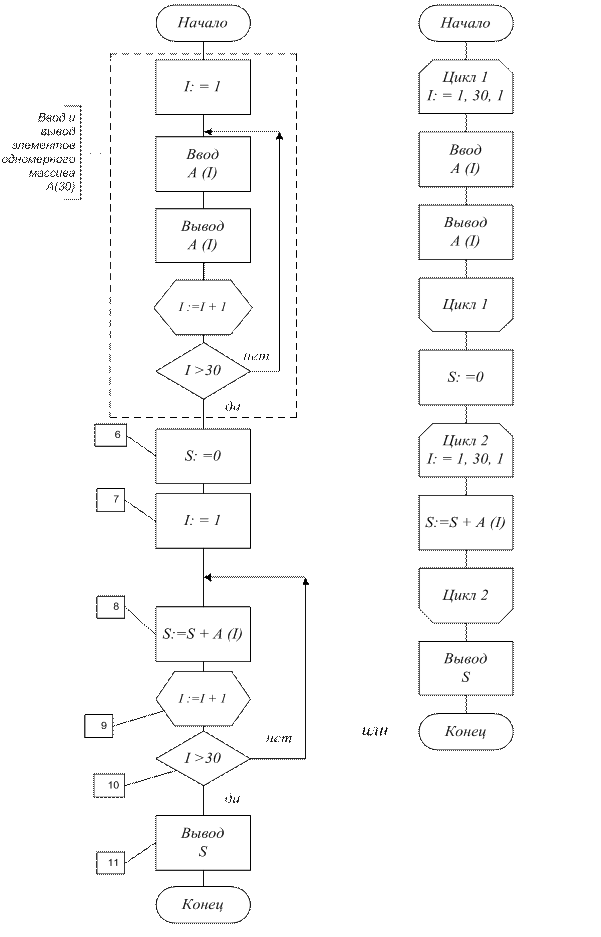
Рис. 35.

Накопление суммы производится путём прибавления очередного слагаемого элемента A (I), где I — текущее значение индекса (номер ячейки), к сумме всех предыдущих слагаемых (блок 8). Здесь важно наличие одного и того же имени переменной S, т. е. новое значение переменной S есть старое значение суммы S (первоначальное значение S=0 – пустая ячейка для накапливания суммы, блок 6), увеличенное на значение очередного слагаемого A(I).

Блок 7 — блок подготовки цикла, текущему значению индекса I присваивается единица для обработки первого элемента массива. При первом прохождении тела цикла (блок 8) новое значение S становится равно 0+ A(1). В блоке 9 (модификация) увеличиваем текущее значение индекса для обработки следующего элемента массива. Это соответствует выбору следующего элемента массива из следующей ячейки памяти.

В блоке 10 проверяем, окончен ли цикл: если I ≠ 31 (на выходе из цикла I=31), то снова выполняем тело цикла. После суммирования всех элементов выводим полученную сумму (блок 11).

Пример 16. Составить схему алгоритма получения произведения P положительных элементов массива и суммы S отрицательных элементов в массиве C(20) (рис. 36).

В блоке 7, входящем в подготовку цикла, начальное значение произведения P = 1. В теле цикла в блоке 10 новое значение произведения получаем увеличением предыдущего значения произведения в C(I) раз.

Блок 9 отсортировывает положительные и отрицательные элементы массива. При выходе из блока по ветке «да» будут перемножаться положительные элементы массива. По ветке «нет» отбираются отрицательные и нулевые элементы, не изменяющие сумму отрицательных элементов, которые и суммируются.

Пример 17. Составить схему алгоритма вычисления значения среднего арифметического отрицательных элементов массива C(1), С(2),..., С(30), полагая, что в массиве есть отрицательные значения (рис. 37).

Чтобы найти среднее арифметическое отрицательных элементов какого-либо массива, надо сумму этих элементов разделить на их количество. Организуем цикл, в котором каждый элемент массива проверяем, отрицателен он или нет (блок 9), и если отрицателен, то искомую сумму S увеличиваем на значение соответствующего элемента массива C(I) (блок 10), а для подсчёта количества K отрицательных членов ставим счётчик (блок 11), где количество отрицательных элементов увеличиваем на единицу. Первоначальные значения S и K обнуляем (блоки 6 и 7).

Если элемент массива не отрицателен, то переходим на блок 12 – блок модификации, подготавливающий выбор и анализ следующего элемента массива, увеличивая I на единицу. Блок 13 – проверка завершения цикла. Если все элементы массива рассмотрены, осуществляем выход из цикла (на выходе из цикла I=31) и рассчитываем среднее арифметическое Sср отрицательных элементов массива (блок 14). В блоке 15 выводим искомые величины S, K, Sср. В данной схеме алгоритма телом цикла являются блоки 9, 10, 11.

Рис. 36.

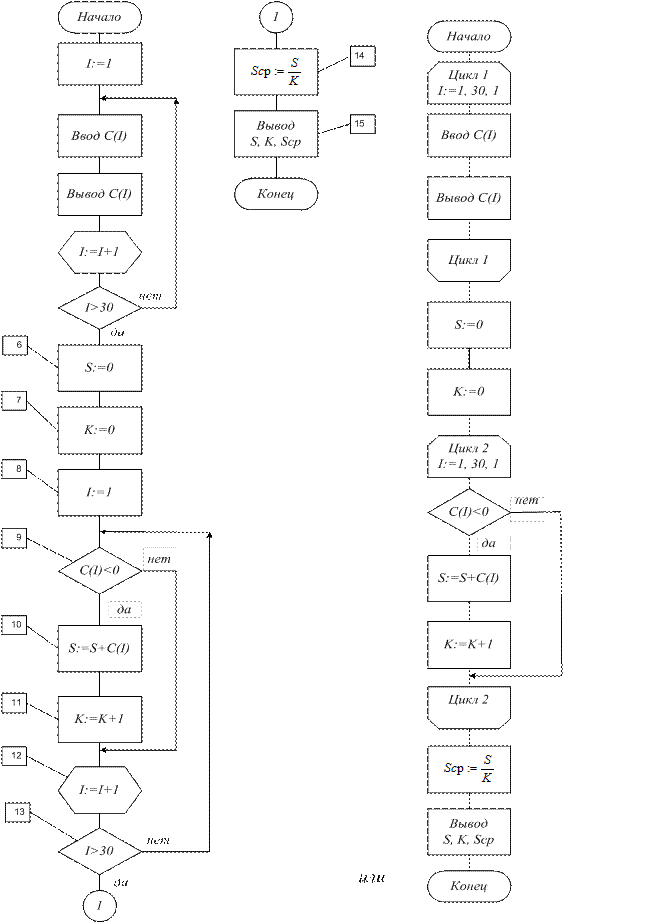Рис. 37.

Пример 18. Составить схему алгоритма вычисления произведения элементов массива C(50), имеющих значения от 0 до 1 и индексы, кратные трем (рис. 38).

Данная задача отличается от задачи нахождения произведения всех элементов массива тем, что элементы, произведение которых требуется получить, должны обеспечить кратность индексов трем.

Первоначальное произведение P равно единице (блок 6). Начинаем рассматривать элементы с элемента с индексом I = 3 (блок 7), и в блоке модификации (блок 11) увеличиваем индекс на три (шаг равен трём). В теле цикла каждый обрабатываемый элемент массива проверяем, имеет ли он значение в промежутке [0; 1] (блоки 8 и 9). Если его значение лежит в этом промежутке, искомое произведение увеличиваем (блок 10), если нет, то переходим к блоку модификации, подготавливая к рассмотрению следующий элемент массива.

Блок 12— блок проверки условия завершения цикла. В блоке 13 выводим значение произведения P.

Пример 19. Дан массив В(100). Составить схему алгоритма, где найти количество нулевых элементов данного массива, а из отрицательных и положительных элементов данного массив сформировать два массива, назвав их соответственно BO и BP (рис. 39).

Присваиваем имена переменным и задаем первоначальные значения: количество нулевых элементов массива K = 0 (блок 5), значения текущих индексов: в массиве BP L=0 (блок 6) и в массиве BO M=0 (блок 7). В теле цикла (блоки 9…17), рассматривая каждый элемент массива, если В(I)>0 (блок 9) увеличиваем счетчик индексов массива BP L на 1 (блок 10) и получаем очередной элемент массива BP(L) (блок 12), если В(I)<0 (блок 13) увеличиваем счетчик индексов массива BO M на 1 (блок 14) и получаем очередной элемент массива BP(M) (блок 16), если В(I)=0 (ветка «нет») увеличиваем счетчик нулевых элементов K на 1 (блок 17). Попутно в блоках 11 и 15 ставим метки C и D для запоминания конечных значений индексов элементов новых массивов. В блоке 19 выводим значение количества K нулевых элементов массива В(100) и организуем два цикла для вывода новых массивов.

Пример 20. В одномерном массиве D(200) найти максимальный элемент и поменять его местами с последним элементом массива (рис. 40).

В данном случае поиск максимального элемента массива выполняется путем сравнения каждого элемента с каким-то значением МАХ, которому для определенности перед началом цикла присваивается значение первого элемента массива D(1) (блок 6). Хотя можно было бы значению МАХ присвоить значение любого элемента массива D(200). В теле цикла, если значение МАХ меньше текущего значения элемента массива D(I) (блок 8), то присваиваем переменной МАХ значение этого элемента (блок 9). Поскольку в последующем требуется поменять местами последний элемент массива D(200) и максимальный элемент, требуется знать индекс (номер ячейки) максимального элемента массива. Для этого вводим переменную K (блок 10), которая после выполнения цикла будет иметь значение индекса максимального элемента в массиве D(200). В блоках 13, 14 производим обмен значениями между последним и максимальным элементами массива. Последовательность блоков 13 и 14 важна, так как если бы сначала элементу D(200) присвоили значение МАХ, то само значение D(200) было бы потеряно. В блоке 15 выводим значение максимального элемента и значение его индекса, также выводим новый массив D(200) после замены в нём элементов.

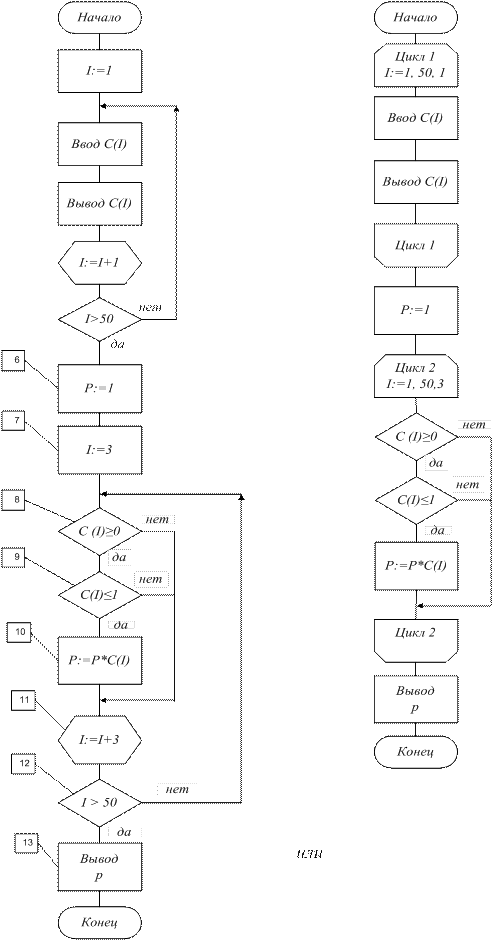
Рис. 38.

Рис. 39.

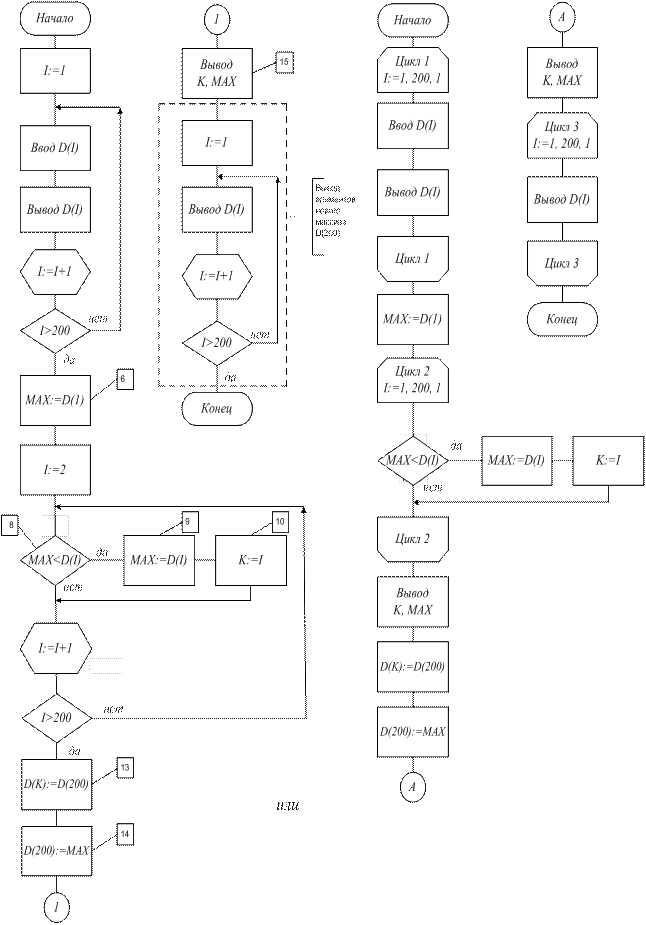
Рис. 40.

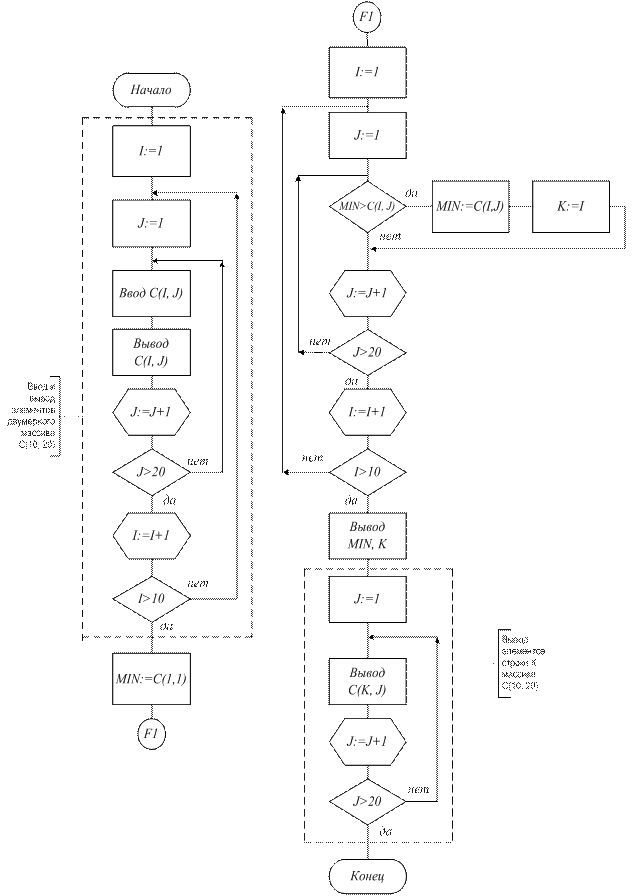
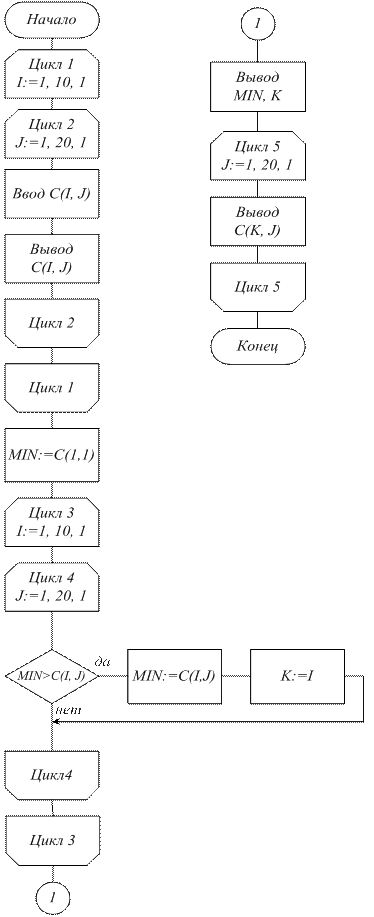
Пример 21. Найти наименьший элемент матрицы C(10, 20) и вывести на печать всю строку, в которой он находится (рис. 41 а, б).

Осуществляем ввод элементов массива C(I, J) при помощи двух циклов (по индексу I и по индексу J). Цикл 2 (по индексу J)является вложенным циклом. Ставим метку К – номер строки, где находится МIN – наименьший элемент массива. Для вывода элементов строки К организуем цикл по индексу J (по столбцам).

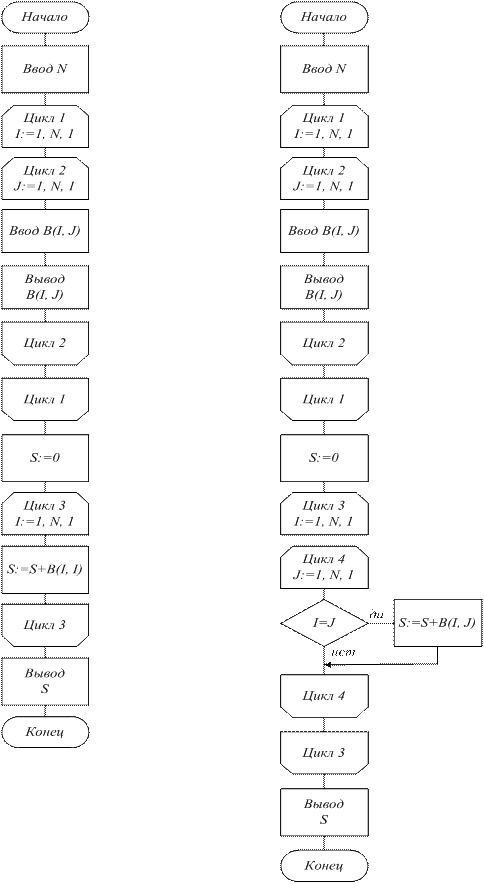
Пример 22. Дана квадратная матрица B(N, N). Требуется найти сумму элементов главной диагонали (рис. 42 а, б).

До ввода элементов матрицы необходимо ввести число N — количество строк и столбцов матрицы B(N, N).

В первом варианте а) организован один цикл по I, так как у элемента главной диагонали квадратной матрицы индексы равны. Во втором варианте б) организованы циклы по каждому индексу элемента матрицы. Какой вариант предпочтительнее, надо решать в каждом конкретном случае.

Пример 23. Дан двумерный массив A(М, N). Требуется вычислить сумму элементов матрицы в каждой строке, а также сформировать из этих сумм одномерный массив В(М) (рис. 43).

Рассматривается задача для матрицы с любым количеством строк и столбцов. Поэтому до ввода элементов самой матрицы должны быть введены значения М и N, определяющие количество строк и столбцов матрицы. Здесь два цикла. Внешний цикл по I, в котором выполняются действия для каждой строки:

— обнуляется сумма (блок 9);

— суммируются все элементы (блок 11);

— выводится получаемая сумма элементов (блок 13).

В блоке 14 формируем одномерный массив В(М), элементы которого являются суммами элементов каждой строки массива A(М, N) и осуществляем его вывод в блоке 15.

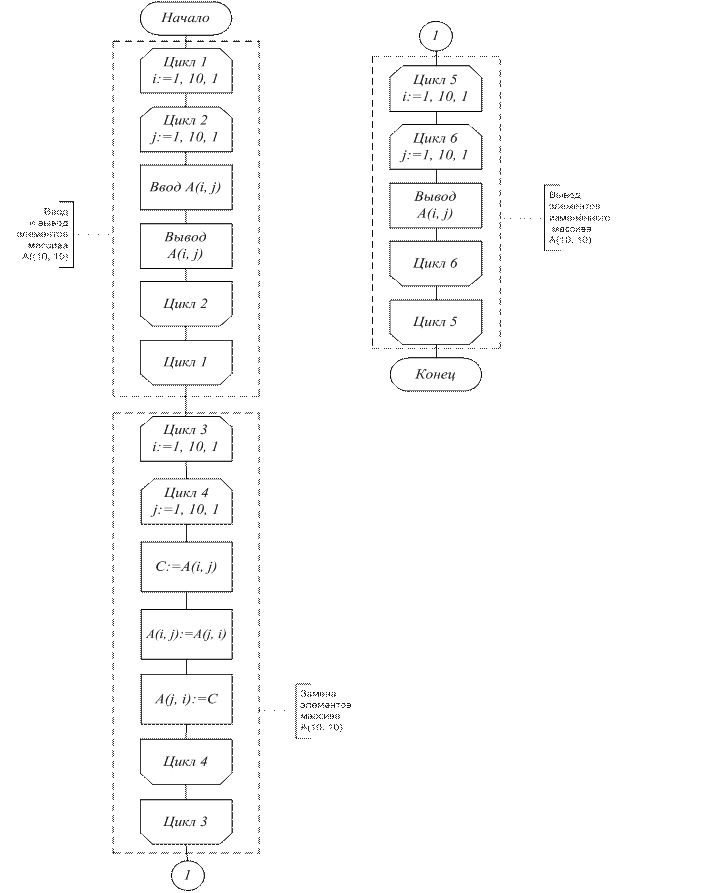
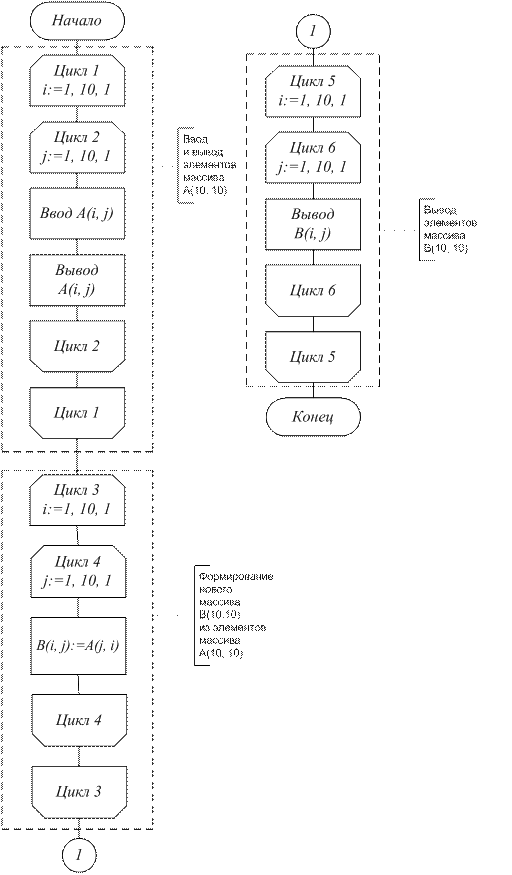
Пример 24. Транспонировать матрицу A(10, 10), т. е. поменять индексы столбцов на индексы строк и наоборот. Требуется поменять местами элементы A(i, j) и A(j, i) (рис. 44 а, б).

Соответствующие приведенным двум вариантам решения задачи программы имеют разное время выполнения и объем необходимой памяти ЭВМ. В первом варианте (см. рис. 44 а) обмен значениями между элементами A(i, j) и A(j, i) производится через одну и ту же ячейку С. Полученная новая матрица А(10, 10) будет занимать в памяти те же ячейки, что и старая А(10, 10). Значения элементов старой матрицы A(10, 10) будут потеряны. Во втором же варианте (см. рис. 44 б) получаем новую матрицу B(10, 10), элементы которой B(i, j) = A(j, i). Этим сохраняем старую матрицу A(10, 10), но дополнительно потребуется память для 100 элементов матрицы B(10, 10).

а)

Рис. 41.

б)

Рис. 41.

а) б)

Рис. 42.

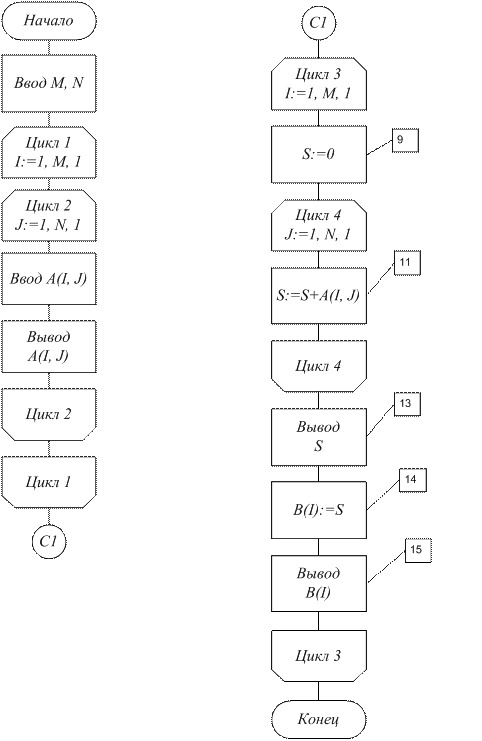
Рис. 43.

а)

Рис. 44.

б)

Рис. 44.

ПРИЛОЖЕНИЕ

Date: 2015-06-06; view: 688; Нарушение авторских прав