Связь напряженности и потенциала

1. Мы уже знаем, как вычислять разность потенциалов по известной напряженности:

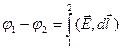. (1)

2. Как решить обратную задачу: зная потенциал, найти напряженность поля?

Запишем для двух бесконечно близких точек 1 и 2:

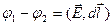, или .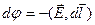

Распишем скалярное произведение через проекции векторов на декартовы оси координат:

,

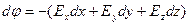Отсюда видно, что:

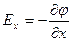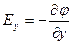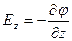, , . (2)

Формулы (2) позволяют найти составляющие вектора 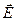по известной функции .

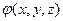В векторном анализе вводится понятие градиента скалярной функции 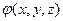: это вектор, составляющие которого равны 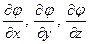. Таким образом, мы можем записать:

.

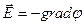(Градиент также обозначается знаком «набла»: ).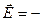

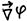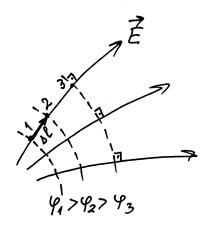Градиент скалярной функции – это вектор, направленный в сторону наиболее быстрого возрастания функции. (Вектор же 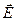, благодаря знаку «минус» перед градиентом, направлен в сторону наиболее быстрого убывания функции.)

Итак, электрическое поле можно описать или через напряженность, или через потенциал. Формулы (1) и (2) позволяют «переводить» описание с одного языка на другой.

Если мы видим картину линий напряженности, мы можем изобразить эквипотенциальные поверхности (на плоскости - линии). И наоборот: по картине эквипотенциальных поверхностей мы можем построить линии напряженности и оценить модуль напряженности. Такую задачу вы выполняете в лабораторной работе 2.3: средняя напряженность поля в области, скажем, между точками 1 и 2:

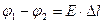
Date: 2015-05-04; view: 898; Нарушение авторских прав