ПИТАННЯ-МІНІМУМ З ФІЗИКИ

1. МЕХАНІКА

1. Що таке рівняння руху? Як знайти за ним швидкість та прискорення?
2. Рівняння рівномірного та рівнозмінного рухів. Фізичний зміст коефіцієнтів в них.
3. Рівняння та графік зміни координати точки, яка здійснює гармонійне коливання. Амплітуда, частота, фаза, початкова фаза.
4. Тангенційне і нормальне прискорення при криволінійному русі.
5. Другий закон Ньютона (основний закон динаміки) у векторній і координатній формах.
6. Імпульс. Закон збереження імпульсу, умови збереження.
7. Робота сили. Елементарна робота і робота на кінцевому переміщенні.
8. Кінетична і потенційна енергія матеріальної точки. Потенційна енергія тіла в полі тяжіння Землі поблизу її поверхні.
9. Закон збереження механічної енергії. Умови збереження.
10. Основне рівняння динаміки обертального руху твердого тіла. Момент інерції.
11. Момент імпульсу. Закон збереження моменту імпульсу.
12. Кінетична енергія і момент імпульсу тіла, що обертається.

2. МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА

1. Поняття і фізичний зміст моля речовини.
2. Визначення і фізичний зміст температури. Зв’язок Т і t.
3. Рівняння стану ідеального газу.
4. Ізопроцеси. Рівняння і графіки в РV-координатах.
5. Адіабатичний процес. Рівняння і графік адіабати.
6. Графік розподілу Максвела молекул за швидкостями. Фізичний зміст функції розподілу f (v).
7. Перший початок термодинаміки. Вирази для внутрішньої енергії, роботи, теплоти.
8. Другий початок термодинаміки (словесні формулювання і формула для ізольованої системи).
9. Цикл Карно. К.к.д. циклу Карно, його зв’язок з к.к.д. реальних двигунів.
10. Рівняння Ван-дер-Ваальса, фізичний зміст його членів.

3. ЕЛЕКТРОСТАТИКА. ПОСТІЙНИЙ СТРУМ

1. Елементарний заряд. Закон збереження електричного заряду.
2. Закон Кулона.
3. Електростатичне поле. Напруженість електростатичного поля.
4. Потенціал електростатичного поля. Різниця потенціалів.
5. Електроємність. Ємність плоского конденсатора. Ємність паралельно та послідовно з’єднаних конденсаторів.
6. Енергія зарядженого конденсатора та електростатичного поля.
7. Електричний струм. Сила струму.
8. Електрорушійна сила джерела та напруга.
9. Закон Ома для ділянки ланцюга і повного ланцюга.
10. Робота і потужність струму. Закон Джоуля-Ленца.
11. Правила Кірхгофа.

4. МАГНЕТИЗМ

1. Магнітне поле, його характеристики. Закон Біо-Савара-Лапласа.
2. Дія магнітного поля на елемент струму. Закон Ампера.
3. Дія магнітного поля на рухомий заряд. Сила Лоренца.
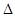
4. Ефект Холла: зміст і формула для _H.
5. Магнітне поле соленоїда (формула для В).
6. Явище електромагнітної індукції. Закон Фарадея.
7. Індуктивність контуру. Самоіндукція.
8. Енергія магнітного поля (формула для соленоїда).
9. Трансформатори.

5. ОПТИКА

1. Електромагнітні хвилі. Їх характеристики: 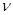, , 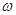, 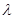T, c, зв’язок між ними.

2. Природне та поляризоване світло. Закон Малюса.

3. Закон заломлення світла: рівняння та рисунок. Повне внутрішнє відбивання світла.

4. Інтерференція світла. Інтерференційна картина для двох щілинних джерел (графік та формула для максимумів).

5. Дифракція світла. Дифракційна гратка: картинка і формула для максимумів.

6. Закони Кірхгофа, Стефана-Больцмана, зміщення Віна.

7. Спектр випромінювання абсолютно чорного тіла. Формула Планка (можна графік для двох Т).

8. Рівняння Ейнштейна для фотоефекта, фізичний зміст його членів. Формули для енергії та імпульсу фотона.

6. АТОМНА ФІЗИКА

1. Співвідношення невизначеностей.
2. Хвилі де Бройля. Хвильова функція. Її фізичний зміст.
3. Спін електрону. Ферміони і бозони. Принцип Паулі.
4. Поглинання та випромінювання світла атомами: другий постулат Бора.
5. Будова атома. Склад ядра. Дефект мас. Енергія зв’язку.
6. Реакції ділення і синтезу: привести по одному прикладу.
7. Радіоактивність: суть явища і закон розпаду.
8. Методи спостереження та реєстрації радіоактивних випромінювань.

ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ З РОЗДІЛІВ МЕХАНІКА, МОЛЕКУЛЯРНА ФІЗИКА, ЕЛЕКТРИКА

Приклад 1. Рівняння руху матеріальної точки вздовж осі має вид х = А + Вt + Ct³, де А = 2 м, В = 1 м/с, С = – 0,5 м/с³. Знайти координату х, швидкість υ та прискорення а в момент часу t = 2 с.

Розв’язок. Координату х знайдемо, підставивши в рівняння руху числові значення коефіцієнтів А, В і С та часу t:

х = (2 + 1 × 2 – 0,5 × 2³) м = 0.

Миттєва швидкість є перша похідна від координати за часом:

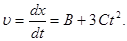
В момент часу t = 2 с.

υ = (1 – 3 × 0,5 × 2²) м/с = – 5 м/с.

Прискорення точки знайдемо, взявши першу похідну від швидкості за часом:

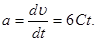
В момент часу t = 2 с.

а = 6 (– 0,5) × 2 м/с² = – 6 м/с².

Приклад 2. Тіло обертається навколо нерухомої осі за законом j = А + Вt + Сt², де А = 10 рад, В = 20 рад/с, С = - 2 рад/с². Знайти повне прискорення точки, яка знаходиться на відстані r = 0,1 м від осі обертання, на момент часу t = 4 с.

Розв’язок. Повне прискорення точки, яка рухається по кривій лінії, може бути знайдено як геометрична сума тангенційного прискорення 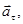яке направлене по дотичній до траєкторії, і нормального прискорення 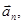направленого до центру кривизни траєкторії (рис. 1).

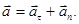
Так як вектори і 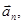взаємно перпендикулярні, то абсолютне значення прискорення

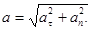(1)

Тангенційне і нормальне прискорення точки тіла яке обертається виражаються формулами:

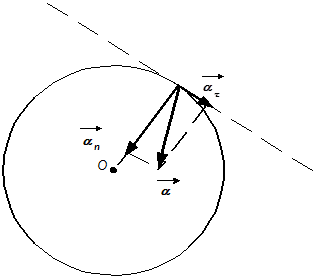
Рисунок 1.

а_t = e r, a_n = w² r,

де w – кутова швидкість тіла;

e - його кутове прискорення.

Підставляючи вираз для а_t і а_n в формулу (1), знаходимо

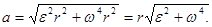(2)

Кутову швидкість w знайдемо, взявши похідну від кута повороту за часом:

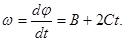
На момент часу t = 4 с кутова швидкість

w = [20 + 2 (-2)× 4] рад/с = 4 рад/с.

Кутове прискорення знайдемо, взявши похідну від кутової швидкості за часом:

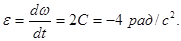
Цей вираз не містить параметру часу; отже, кутове прискорення заданого руху постійне. Підставляючи знайдені значення w і e і задане значення r в формулу (2), отримаємо

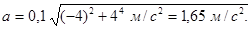
Приклад 3. Ящик масою m₁ = 20 кг зісковзується по ідеально гладкому лотку довжиною l = 2 м на нерухомий візок з піском і застряє в ньому. Візок з піском масою m₂ = 80 кг може вільно (без тертя) переміщуватись по рейках в горизонтальному напрямку. Визначити швидкість и візка з ящиком, якщо лоток нахилений під кутом a = 30⁰ до рейок.

Розв’язок. Візок і ящик можна розглядати як систему двох тіл, які непружньо взаємодіють. Але ця система не замкнена, так як сума зовнішніх сил, яка діє на систему: двох сил тяжіння 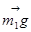і та сили реакції 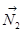(рис. 2) не дорівнює нулю. Тому застосувати закон збереження імпульсу до системи ящик-візок не можна. Але так як проекція суми вказаних сил на напрямок осі х, яка співпадає з напрямком рейок, дорівнює нулю, складову імпульсу системи в цьому напрямку можна вважати постійною, тобто

Рисунок 2.

р_1х + р_2х = р^/_1х + р^/_2х, (1)

де р_1х і р_2х – проекції імпульсу ящика і візка з піском в момент падіння ящика на візок;

р^/_1х і р^/_2х – ті самі величини після падіння ящика.

Виразимо в рівнянні (1) імпульси тіл через їх маси і швидкості, враховуючи, що р_2х = 0 (візок до взаємодії з ящиком покоївся), а також той факт, що після взаємодії обидва тіла системи рухаються з однією швидкістю и:

m₁υ_ix = (m₁ + m₂) и,

або

m₁υ_i cos a = (m₁ + m₂) и,

де υ_i – швидкість ящика перед падінням на візок;

υ_ix = υ_i cos a – проекція цієї швидкості на вісь х.

Звідси виразимо шукану швидкість:

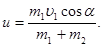(2)

Швидкість υ₁ визначимо за законом збереження енергії:

,

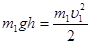де h = l sin a. Після скорочення на m₁ знайдемо

Підставивши визначений вираз υ₁ в формулу (2), одержимо:

Підставимо сюди числові значення величин і проведемо розрахунки:

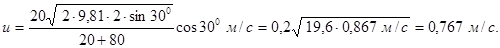
Приклад 4. Через блок у вигляді суцільного диска, який має масу m = 80 г (рис. 3), перекинута тонка, гнучка нитка, до кінців якої підвішені вантажі з масами m₁ = 100 г і m₂ = 200 г. З яким прискоренням будуть рухатись вантажі самі по собі? Тертям і масою нитки знехтувати.

Розв’язок. Скористаємося основними рівняннями динаміки поступального і обертального рухів. Для цього розглянемо сили, які діють на кожний з вантажів і на блок окремо. На перший вантаж діють дві сили: сила тяжіння 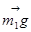і сила пружності (сила натягу нитки) Спроектуємо ці сили на вісь х, яку направимо вниз, і напишемо рівняння руху (другий закон Ньютона) в координатній формі:

m₁g – T₁ = -m₁a. (1)

Рівняння руху для другого вантажу запишеться аналогічно:

m₂g – T₂ = -m₂a. (2)

Під дією двох моментів сил і відносно осі, перпендикулярної площині креслення, блок отримає кутове прискорення e (e = а / r). Згідно основного рівняння динаміки обертального руху

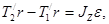(3)

Рисунок 3.

де 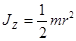– момент інерції блоку (суцільного диску) відносно до осі Z.

Сила 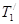згідно третьому закону Ньютона за абсолютним значенням дорівнює силі Т₁. Відповідно сила за абсолютним значенням дорівнює силі Т₂. Скориставшись цим, підставимо в рівняння (3) замість 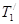і вираз для Т₁ і Т₂, які ми отримали попередньо з рівнянь (1) і (2):

Після скорочення на r та перегрупування членів знайдемо прискорення, яке нас цікавить:

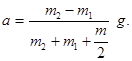(4)

Відношення мас в правій частині формули (4) є величина безрозмірна. Тому маси m₁, m₂ і m можна виразити в грамах, як вони надані в умові задачі. Прискорення треба виразити в одиницях СІ. Після підстановки одержимо

Приклад 5. Платформа у вигляді суцільного диска радіусом R = 1,5 м і масою m₁ = 180 кг обертається за інерцією навколо вертикальної осі з частотою n = 10 хв^-1. В центрі платформи стоїть людина масою m₂ = 60 кг. Яку лінійну швидкість відносно підлоги приміщення буде мати людина, якщо вона перейде на край платформи?

Розв’язок. Платформа обертається за інерцією. Отже момент зовнішніх сил відносно осі обертання Z, яка співпадає з геометричною віссю платформи, дорівнює нуля. При цій умові момент імпульсу L_Z системи платформа – людина залишається постійною:

L_Z = J_Zw = const, (1)

де J_Z – момент інерції платформи з людиною відносно осі Z;

w – кутова швидкість платформи.

Момент інерції системи дорівнює сумі моментів інерції тіл, які входять до складу системи, тому J_Z = J₁ + J₂, де J₁ – момент інерції платформи; J₂ – момент інерції людини.

З урахуванням цього рівняння (1) буде мати вид

(J₁ + J₂) w = const,

або

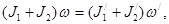(2)

де значення моментів інерції J₁ і J₂ відносяться до початкового стану системи; 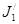і 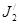- до кінцевого.

Момент інерції платформи відносно осі Z при переході людини не зміниться: 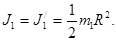Момент інерції людини відносно тієї самої осі буде змінюватись. Якщо розглядати людину як матеріальну точку, то її момент інерції J₂ в початковому положенні (в центрі платформи) можна рахувати рівним нулю. В кінцевому положенні (на краю платформи) момент інерції людини 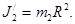Підставимо у формулу (2) знайдені вирази моментів інерції, а також виразимо початкову кутову швидкість w обертання платформи з людиною через частоту обертання n (w = 2pn) і кінцеву кутову швидкість w^/ – через лінійну швидкість v людини відносно підлоги (w^/ = u/R):

Після скорочення на R² та простих перетворень знаходимо швидкість, яка нас цікавить:

Враховуючи, що n = 10 хв^-1 = 1/6 с^-1, підставимо числові значення фізичних величин в СІ та проведемо обчислення:

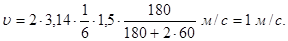
Приклад 6. Точка здійснює гармонійні коливання з частотою n = 10 Гц. В момент, прийнятий за початковий, точка мала максимальне зміщення х_max = 1 мм. Написати рівняння коливань точки і накреслити їх графік.

Розв’язок. Рівняння коливань точки можна записати у вигляді

х = Аsin (wt + j₁), (1)

або

х = Аcos (wt + j₂), (2)

де А – амплітуда коливань;

w – циклічна частота;

t – час;

j₁ і j₂ – початкові фази.

За визначенням, амплітуда коливань

А = х_max. (3)

Циклічна частота w пов’язана з частотою n співвідношенням

w = 2pn. (4)

Початкова фаза коливань залежить від форми запису. Якщо використати форму (1), то початкову фазу можна визначити із умови: в момент t = 0

x_max = Asin j₁,

звідки

або

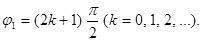
Зміна фази на 2p не змінює стану коливального руху, тому можна прийняти

j₁ = p / 2. (5)

У випадку другої форми запису отримуємо

або

j₂ = 2 pk (k = 0, 1, 2, 3, …).

По тим самим міркуванням, що і в першому випадку, знаходимо

j₂ = 0. (6)

З урахуванням рівнянь (3) – (6) рівняння коливань будуть мати вид:

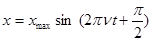
або

x = x_max cos 2 pnt,

де х_max = 1 мм = 10^-3 м; n = 10 Гц.

Графік відповідного гармонічного коливання приведений на рис. 4.

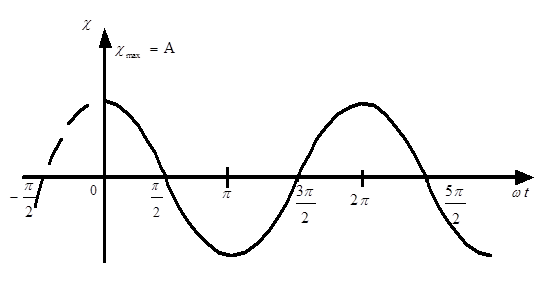
Рисунок 4.

Приклад 7. Визначити число N молекул, які містяться в об’ємі V = 1 мм³ води, і масу m₁ молекули води. Враховуючи умовно, що молекули води мають вид кульок, що щільно прилягають одна до одної, знайти діаметр d молекул.

Розв’язок. Число N молекул, які містяться в деякій масі m, дорівнює добутку числа Авогадро N_A на кількість речовини n в молях

N = nN_A.

Так як кількість речовини

n = m / m,

де m – молярна маса, то

Виразивши в цій формулі масу як добуток густини на об’єм V, отримаємо

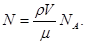(1)

Підставимо в формулу (1) такі значення величин: r = 10³ кг/м³; V = 1 мм³ = 10^-9 м³; m = 18 × 10^-3 кг/моль; N_А = 6,02× 10²³ моль^-1 і проведемо розрахунки:

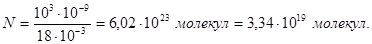
Масу m₁ однієї молекули можна знайти діленням молярної маси на число Авогадро:

Підставивши сюди числові значення m і N, знайдемо масу молекули води:

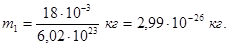
Якщо молекули води щільно прилягають одна до одної, то можна рахувати, що на кожну молекулу припадає об’єм (кубічний осередок) V₁ = d³, де d – діаметр молекули. Звідси

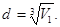(2)

Об’єм V₁ знайдемо, поділивши молярний об’єм V_m на число молекул в молі, тобто на число Авогадро N_A:

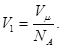
Підставимо отриманий вираз V₁ у формулу (2):

Молярний об’єм, який входить в цю формулу, визначається виразом V_m = m / r. Тоді шуканий діаметр молекули

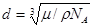. (3)

Перевіримо, чи дає права частина виразу (3) одиницю довжини:

Тепер підставимо числові значення фізичних величин у формулу (3) і проведемо розрахунки:

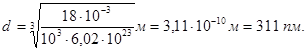
Приклад 8. Балон містить m₁ = 80 г кисню і m₂ = 320 г аргону. Тиск суміші р = 1 МПа, температура Т = 300 К. Приймаючи дані гази за ідеальні, визначити об’єм V балона.

Розв’язок. За законом Дальтона, тиск суміші дорівнює сумі парціальних тисків газів, які входять до складу суміші. Парціальним тиском газу називається тиск, який би створював цей газ, якщо б тільки він один знаходився в посудині, яка зайнята сумішшю.

За рівнянням стану ідеального газу, парціальні тиски кисню р₁ і аргону р₂ виражаються формулами:

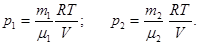
Отже, за законом Дальтона тиск суміші газів

р = р₁ + р₂, або ,

звідки об’єм балону

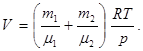(1)

Виразимо в одиницях СІ числові значення величин, які входять в цю формулу: m₁ = 80 г = 0,08 кг; m₁ = 32 × 10^-3 кг/моль; m₂ = 320 г = 0,32 кг; m₂ = 40 × 10^-3 кг/моль; р = 1 Мпа = 10⁶ Па; R = 8,31 Дж / (моль×К).

Підставимо числові значення у формулу (1) і проведемо обчислення:

Приклад 9. Кисень масою m = 2 кг займає об’єм V₁ = 1 м³ і знаходиться під тиском р₁ = 0,2 МПа. Газ був нагрітий спочатку при постійному тиску до об’єму V₂ = 3 м³, а потім при постійному об’ємі до тиску р₃ = 0,5 МПа. Знайти зміну DU внутрішньої енергії газу, здійснену ним роботу А і теплоту Q, передану газу. Побудувати графік процесу.

Розв’язок.. Зміна внутрішньої енергії газу виражається формулою

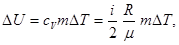(1)

де і – число ступенів свободи молекули газу (для двохатомних молекул кисню і = 5);

μ – молярна маса.

Початкову і кінцеву температуру газу знайдемо з рівняння стану ідеального газу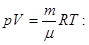

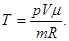(2)

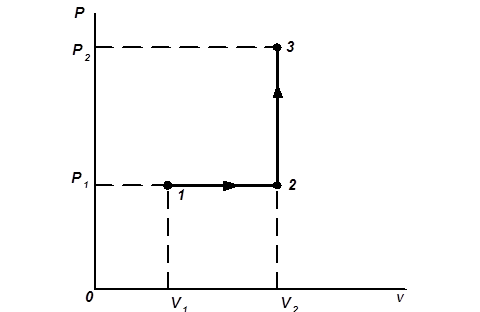
Рисунок 5.

Випишемо задані величини в одиницях СІ: m = 2 кг, m = 32 × 10^-3 кг/моль, R = 8,31 Дж / (моль × К), V₁ = 1 м³, V₂ = V₃ = 3 м³, р₁ = р₂ = 0,2 МПа = 2 × 10⁵ Па, р₃ = 0,5 МПа = 5 × 10⁵ Па. Підставляючи ці значення у вираз (2) і виконуючи арифметичні дії, отримаємо:

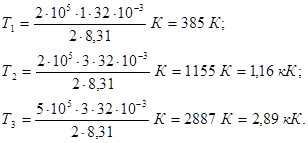
Підставляючи у вираз (1) числові значення величин, які входять в нього, і виконуючи арифметичні дії, знаходимо

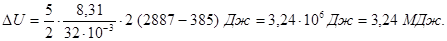
Робота розширення газу при постійному тиску виражається формулою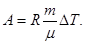

Підставивши числові значення величин, отримаємо

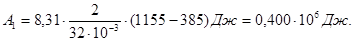
Робота газу, який нагрівається при постійному об’ємі, дорівнює нулю, тобто А₂ = 0. Отже, повна робота, здійснена газом, дорівнює А = А₁ + А₂ = 0,4 × 10⁶ Дж.

Згідно першого початку термодинаміки, теплота Q, передана газу, дорівнює сумі зміни внутрішньої енергії DU і роботи А: Q = DU + A, таким чином, Q = 0,4 × 10⁶ Дж + 3,24 × 10⁶ Дж = 3,64 × 10⁶ Дж = 3,64 МДж.

Графік процесу представлено на рис. 5.

Приклад 10. В циліндрі під поршнем знаходиться водень масою m = 0,02 кг при температурі Т = 300 К. Водень спочатку розширився адіабатично, збільшивши свій об’єм в n₁ = 5 разів, а потім був стиснутий ізотермічно, причому об’єм газу зменшився в n₂ = 5 разів. Знайти температуру в кінці адіабатичного розширення і роботу, здійснену газом при цих процесах. Зобразити процес графічно.

Розв’язок. Температура і об’єм газу, який здійснює адіабатичний процес, пов’язані між собою співвідношенням

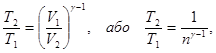
де g – відношення теплоємності газу при постійному тиску і постійному об’ємі (для водню як двохатомного газу g = 1,4);

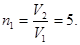
Звідси отримуємо наступний вираз для кінцевої температури Т₂:

Підставляючи числові значення заданих величин, знаходимо

Так як 5^0,4 = 1,91 (знаходиться логарифмуванням), то

Робота А₁ газу при адіабатичному розширенні може бути визначена за формулою:

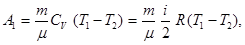
де С_V – молярна теплоємність газу при постійному об’ємі.

Підставивши числові значення величин: R = 8,31 Дж / (моль × К), і = 5 (для водню як двохатомного газу), m = 2 × 10^-3 кг/моль, m = 0,02 кг, Т₁ = 300 К, Т₂ = 157 К у праву частину останньої формули і виконуючи арифметичні дії, одержимо

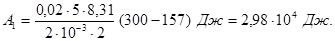
Робота А₂ газу при ізотермічному процесі може бути виражена у вигляді

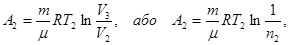
де n₂ = V₂ / V₃ = 5.

Підставляючи відомі числові значення величин, які входять в праву частину цього рівняння, і виконуючи арифметичні дії, знаходимо

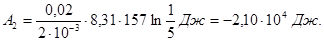
Знак “мінус” показує, що при стисканні робота здійснюється над газом зовнішніми силами. Графік процесу представлено на рис. 6.

Рисунок 6.

Приклад 11. Три точкові заряди Q₁ = Q₂ = Q₃ = 1 нКл розташовані в вершинах рівностороннього трикутника. Який заряд Q₄ треба помістити в центрі трикутника, щоб вказана система зарядів знаходилась у рівновазі?

Розв’язок. Всі три заряди, які розташовані у вершинах трикутника, знаходяться в однакових умовах. Тому достатньо з’ясувати, який заряд слід помістити в центрі трикутника, щоб який-небудь один з трьох зарядів, наприклад Q₁, знаходився в рівновазі. Заряд Q₁ буде знаходитись в рівновазі, якщо векторна сума сил, які діють на нього, дорівнює нулю (рис. 7):

(1)

де - сили, з якими відповідно діють на заряд Q₁ заряди Q₂, Q₃, Q₄;

- рівнодіюча сил

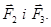
Так як сили 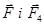направлені по одній прямій в протилежні сторони, то векторне рівняння (1) можна замінити скалярним рівнянням F – F₄ = 0, звідки

F₄ = F.

Виразивши в останньому рівнянні F через F₂ і F₃ і враховуючи, що F₃ = F₂, одержимо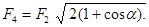

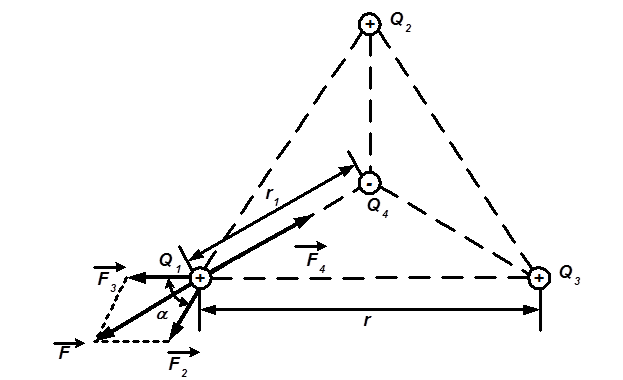Рисунок 7.

Застосовуючи закон Кулона і маючи на увазі, що Q₂ = Q₃ = Q₁, знайдемо

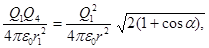
звідки

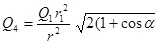. (2)

З геометричних побудувань в рівносторонньому трикутнику слідує, що

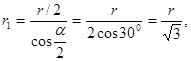
cos a = cos 60⁰ = ½.

З врахуванням цього формула (2) буде мати вид

Підставивши сюди числове значення Q₁ = 1 нКл = 10^-9 Кл, одержимо

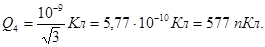
Слід відмітити, що рівновага системи зарядів буде нестійкою.

Приклад 12. Два точкові електричні заряди Q₁ = 1 нКл і Q₂ = -2 нКл знаходяться в повітрі на відстані d = 10 см один від одного. Визначити напруженість 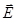і потенціал j поля, яке створюється цими зарядами в точці А, віддаленій від заряду Q₁ на відстань r₁ = 9 см і від заряду Q₂ на r₂ = 7 см.

Розв’язок. Згідно принципу суперпозиції електричних полів, кожний заряд створює поле незалежно від присутності в просторі інших зарядів. Тому напруженість 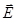електричного поля в шуканій точці може бути знайдена як геометрична сума напруженостей 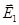і полів, які створюються кожним зарядом окремо: . Напруженість електричного поля, яке створюється в повітрі (e = 1) зарядом Q₁, дорівнює

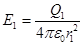, (1)

зарядом Q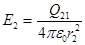₂ –

. (2)

Вектор 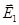(рис. 8) направлений за силовою лінією від заряду Q₁, так як заряд Q₁ позитивний; вектор направлений до заряду Q₂, так як заряд Q₂ негативний.

Рисунок 8.

Абсолютне значення вектора 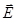знайдемо за теоремою косинусів:

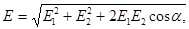(3)

де a - кут між векторами Е₁ і Е₂, який може бути знайдений із трикутника зі сторонами r₁, r₂ і d:

.

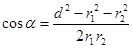В даному випадку щоб уникнути громіздких записів зручно значення cos a обчислювати окремо:

Підставляючи вираз Е₁ із формули (1) і Е₂ із формули (2) в рівняння (3) і виносячи загальний множник ¼ pe₀ за знак кореня, одержимо:

(4)

Підставимо числові значення величин в формулу (4) і проведемо обчислення:

=3,58 × 10³ В/м = 3,58 кВ/м.

При обчисленні Е знак заряду Q₂ опущений, так як знак заряду визначає напрямок вектора напруженості, а напрямок було враховано при його графічному зображенні. (рис. 8).

У відповідності з принципом суперпозиції електричних полів потенціал j результуючого поля, створеного двома зарядами Q₁ i Q₂, дорівнює алгебраїчній сумі потенціалів, тобто

j = j₁ + j₂. (5)

Потенціал електричного поля, яке створюється в вакуумі точеним зарядом Q на відстані r від нього, виражається формулою

(6)

В нашому випадку згідно формулам (5) і (6) одержимо

або

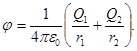
Підставивши в цей вираз числові значення фізичних величин, одержимо

Приклад 13. Конденсатор ємністю С₁ = 3 мкФ був заряджений до різниці потенціалів U₁ = 40 В. Після вимкнення від джерела струму конденсатор був з’єднаний паралельно з іншим незарядженим конденсатором ємністю С₂ = 5 мкФ. Яка енергія W₁ витратиться на створення іскри в момент приєднання другого конденсатора?

Розв’язок. Енергія W₁, що витрачена на створення іскри,

W^/ = W₁ – W₂, (1)

де W₁ – енергія, яку мав перший конденсатор до приєднання до нього другого конденсатора;

W₂ – енергія, яку має батарея, що складена з першого і другого конденсаторів.

Енергія зарядженого конденсаторавизначається за формулою:

(2)

де С – ємність конденсатора або батареї конденсаторів;

U – різниця потенціалів на обкладках конденсаторів.

Виразивши в формулі (1) енергії W₁ i W₂ за формулою (2) і беручи до уваги, що загальна ємність паралельно з’єднаних конденсаторів дорівнює сумі ємностей окремих конденсаторів, отримаємо

, (3)

де U₂ – різність потенціалів на затисках батареї конденсаторів.

Враховуючи, що заряд після приєднання другого конденсатора залишився таким самим, виразимо різницю потенціалів U₂ наступним чином:

Підставивши вираз U₂ в формулу (3), одержимо

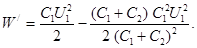
Після простих перетворень знайдемо

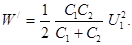
В отриманий вираз підставимо числові значення і обчислимо W^/:

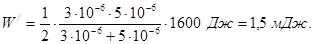
Приклад 14. Сила струму в провіднику опором r = 20 Ом збільшується на протязі часу Dt = 2 с за лінійним законом від І_o = 0 до І = 6 А (рис. 9). Визначити теплоту Q₁, що виділилась в цьому провіднику за першу секунду, і Q₂ – за другу, а також знайти відношення Q₂/ Q₁.

Розв’язок. Закон Джоуля-Ленца у вигляді Q = І² r t справедливий для випадку постійного струму (І = const). Якщо ж сила струму в провіднику змінюється, то вказаний закон справедливий для нескінченно малого відрізку часу і записується у вигляді

dQ = І² rdt. (1)

Тут сила струму І є деякою функцією часу. В нашому випадку

І = kt, (2)

де k – коефіцієнт пропорційності, що чисельно дорівнює збільшенню сили струму за одиницю часу, тобто

Рисунок 9.

З урахуванням (2) формула (1) буде мати вид

dQ = k² rt² dt. (3)

Для визначення теплоти, що виділилась за кінцевий відрізок часу Dt, вираз (3) треба про інтегрувати в межах від t₁ до t₂:

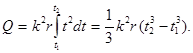
При визначенні теплоти, що виділилась за першу секунду, межі інтегрування t₁ = 0, t₂ = 1 с і, тоді

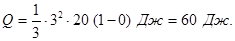
При визначенні теплоти Q₂ межі інтегрування t₁ = 1 c, t₂ = 2 c, тоді

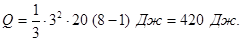
Отже, Q₂/Q₁ = 420 / 60 = 7, тобто за другу секунду виділиться теплоти в 7 разів більше, ніж за першу.

Приклад 15. Електричний ланцюжок складається з двох гальванічних елементів, трьох опорів та гальванометра (рис. 10). В цьому ланцюжку r₁ = 100 Ом, r₂ = 50 Ом, r₃ = 20 Ом, е.р.с. елементу e₁ = 2 В. Гальванометр реєструє струм І₃ = 50 мА, що протікає в напрямку, указаному стрілкою. Визначити е.р.с. e₂ другого елементу. Опором гальванометру і внутрішнім опором знехтувати.

В к а з і в к а. Для розрахунку розгалужених ланцюгів застосовуються правила Кірхгофа.

Перше правило Кірхгофа. Алгебраїчна сума сил струмів у вузлі дорівнює нулю, тобто SІ_і = 0.

Друге правило Кірхгофа. В будь-якому замкненому контурі алгебраїчна сума напруг на окремих ділянках ланцюгу дорівнює алгебраїчній сумі е.р.с., що зустрічаються в контурі.

На підставі цих правил можна скласти рівняння, необхідні для визначення шуканих величин (сил струмів, опорів і е.р.с.). Застосовуючи правила Кірхгофа, слід дотримуватись наступного порядку:

1. Перед складанням рівнянь довільно вибрати: а) напрям струмів (якщо вони не задані за умовою задачі) і вказати їх стрілками на кресленні; б) напрям обходу контурів.

2. При складанні рівнянь за першим правилом Кірхгофа рахувати струми, що підходять до вузла, позитивними; струми, що відходять від вузла, негативними. Число рівнянь повинно бути на одиницю менше від числа вузлів, що знаходяться в ланцюгу.

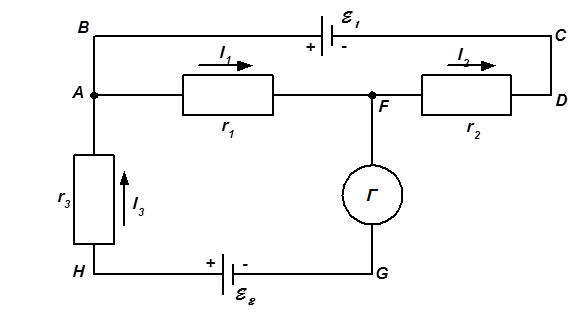
Рисунок 10.

3. При складанні рівнянь за другим правилом Кірхгофа потрібно враховувати, що: а) падіння напруги на ділянці ланцюга (тобто добуток Іr) входить в рівняння зі знаком плюс, якщо напрям струму на даній ділянці співпадає з вибраним напрямом обходу контуру; в противному випадку добуток Іr входить в рівняння зі знаком мінус; б) е.р.с. входить в рівняння зі знаком плюс, якщо вона підвищує потенціал в напрямку обходу контуру, тобто якщо при обході приходиться йти від мінусу до плюсу всередині джерела струму; в противному випадку е.р.с. входить в рівняння зі знаком мінус.

Число незалежних рівнянь, які можуть бути складені за другим правилом Кірхгофа, повинно бути менше від числа замкнених контурів, що є в ланцюгу. Для складання рівнянь перший контур можна вибирати довільно. Всі послідуючі контури потрібно вибирати таким чином, щоб в кожний новий контур входила хоча б одна гілка ланцюгу, яка не брала участі ні в одному із раніше використаних контурів. Якщо при обчисленні рівнянь, складених вказаним вище способом, отримані негативні значення сили струму або опору, то це означає, що струм через даний опір в дійсності тече в напрямку, протилежному довільно вибраному.

Розв’язок. Виберемо напрями струмів, як вони показані на рис., і домовимося обходити контури за годинниковою стрілкою.

За першим правилом Кірхгофа для вузла F маємо

І₁ – І₂ – І₃ = 0. (1)

За другим правилом Кірхгофа маємо для контуру АВСDFA

– І₁r₁ – I₂r₂ = – e₁,

або після помноження обох частин рівняння на –1

І₁r₁ + I₂r₂ = e₁. (2)

Відповідно для контуру АFGHA

І₁r₁ + I₃ r₃ = e₂. (3)

Після підставлення числових значень в формули (1), (2) і (3) отримаємо:

І₁ – І₂ – 0,05 = 0;

50І₁ + 25І₂ = 1;

100І₁ + 0,05 × 20 = e₂.

Переносячи з цих рівнянь невідомі величини в ліві частини, а відомі – в праві, отримаємо наступну систему рівнянь:

І₁ – І₂ = 0,05;

50І₁ + 25І₂ = 1;

100І₁ – e₂ = –1.

Цю систему з трьома невідомими можна розв’язати звичайними прийомами алгебри, але так як за умовою задачі потрібно визначити тільки одне невідоме e₂ з трьох, то скористаємося методом визначників.

Складемо і обчислимо визначник D системи:

Складемо та обчислимо визначник De₂:

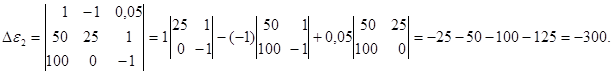
Поділивши визначник De₂ на визначник D, знайдемо числове значення е.р.с. e₂:

e₂ = -300 / -75 = 4 В.

Date: 2015-11-15; view: 509; Нарушение авторских прав