
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Варіант 9
|
|
ЗАДАЧА 1. Диск радіусом R = 0,2 м обертається відповідно рівнянню j = А + Вt + Сt3, де А = 3 рад; В = -1 рад/с; С = 0,1 рад/с3. Визначити тангенційне аt, нормальне аn і повне а прискорення точок на ободі диска для моменту часу t = 10 с.
ЗАДАЧА 2. Куля масою т1 = 5 кг рухається зі швидкістю υ 1 = 1 м/с і зіштовхується з кулею яка перебуває в спокої масою m2 = 2 кг. Визначити швидкості u1 і u2 куль після удару. Кулі вважати однорідними, абсолютно пружними, удар – прямим, центральним.
ЗАДАЧА 3. Налетівши на пружинний буфер, вагон масою m = 16 т, який рухався зі швидкістю υ = 0,6 м/с, зупинився, стиснувши пружину на DL = 8 см. Знайти загальну жорсткість k пружин буфера.
ЗАДАЧА 4. Блок, який має форму диска масою m = 0,4 кг, обертається під дією сили натягу нитки, до кінців якої підвішені тягарі масою m1 = 0,3 кг і m2 = 0,7 кг. Визначити сили Т1 і T2 натягу нитки по обидві сторони блока.
ЗАДАЧА 5. Визначити лінійну та кутову швидкості супутника Землі, який обертається по колу на висоті 1000 км.
ЗАДАЧА 6. У балоні об'ємом V = 3 л утримується кисень масою m = 10 г. Визначити концентрацію n молекул газу.
ЗАДАЧА 7. Визначити густину r водяної пари, яка знаходиться під тиском р = 2,5 кПа при температурі Т = 250 К.
ЗАДАЧА 8. Одноатомний газ при нормальних умовах займає об'єм V = 5 л. Обчислити теплоємність СV цього газу при постійному об'ємі.
ЗАДАЧА 9. У балоні при температурі Т1 = 145 К і тиску р1 = 2 МПа знаходиться кисень. Визначити температуру Т2 і тиск р2 кисню після того, як з балона буде дуже швидко випущена половина газу.
ЗАДАЧА 10. Здійснюючи цикл Карно, газ отримав від нагрівача теплоту Q1 = 500 Дж і здійснив роботу А = 100 Дж. Температура нагрівача Т1 = 400 К. Визначити температуру T2 охолоджувача.
ЗАДАЧА 11. Два позитивних точкових заряди Q і 9Q закріплені на відстані L = 100 см один від одного. Визначити, в якій точці на прямій, яка проходить через заряди, слід помістити третій заряд так, щоб він знаходився у рівновазі.
Вказати, який знак повинен мати цей заряд для того, щоб рівновага була стійкою, якщо переміщення заряду можливе тільки уздовж прямої, яка проходить через закріплені заряди.
ЗАДАЧА 12. Електрон, який має кінетичну енергію Т = 10 еВ, влетів в однорідне електричне поле у напрямку силових ліній поля. Яку швидкість буде мати електрон, пройшовши в цьому полі різницю потенціалів U = 8 В?
ЗАДАЧА 13. Від батареї, е.р.с. якої ξ = 600 В, потрібно передати енергію на відстань L = 1 км. Потужність споживача Р = 5 кВт. Знайти мінімальні втрати потужності у мережі, якщо діаметр мідного підвідного дроту d = 0,5 см.
ЗАДАЧА 14. Визначити різницю потенціалів між точками А і В (див. рис.), якщо ξ1 = 8 В, ξ2 = 6 В, r1 = 4 Ом, r2 = 6 Ом, r3 = 8 Ом. Внутрішніми опорами джерел струму знехтувати.
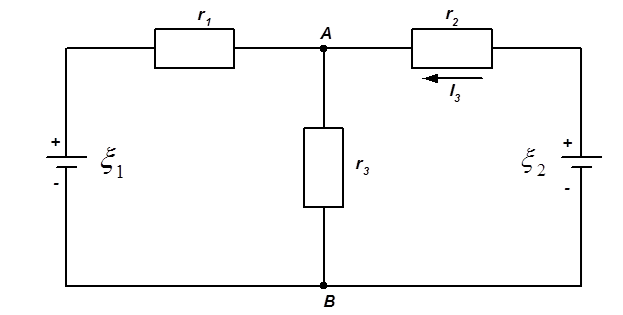
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ З РОЗДІЛІВ МАГНЕТИЗМ, ОПТИКА, АТОМНА ФІЗИКА
Приклад 1. Два паралельні нескінченно довгі дроти D і С, у яких течуть в одному напрямку електричні струми силою І = 60 А, розміщені на відстані d = 10 см один від одного. Визначити магнітну індукцію  поля, що створюється провідниками зі струмом в точці А (рис. 1), що віддалена від осі одного провідника на відстань r1 = 5 см, від другого – r2 = 12 см.
поля, що створюється провідниками зі струмом в точці А (рис. 1), що віддалена від осі одного провідника на відстань r1 = 5 см, від другого – r2 = 12 см.

Рисунок 1.
Розв’язок. Для знаходження магнітної індукції  в точці А скористаємось принципом суперпозиції магнітних полів. Для цього визначимо напрямок магнітної індукції
в точці А скористаємось принципом суперпозиції магнітних полів. Для цього визначимо напрямок магнітної індукції 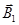 і
і 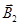 полів, що створюються кожним провідником зі струмом окремо, і складемо їх геометрично:
полів, що створюються кожним провідником зі струмом окремо, і складемо їх геометрично:
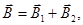
Абсолютне значення магнітної індукції В може бути знайдено за теоремою косинусів:
 (1)
(1)
де a - кут між векторами 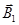 і
і 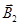 .
.
Значення магнітних індукцій* В1 і В2 виражаються відповідно через силу струму І і відстані r1 і r2 від дротів до точки А:
В1 = m0 І / 2pr1; В2 = m0 І / 2pr2.
Підставляючи вирази В1 і В2 в формулу (1) і виносячи m0 І / 2p за знак кореня, отримаємо:
 (2)
(2)
Обчислимо cos a. Помітивши, що a = ÐDAC (як кути зі взаємно перпендикулярними сторонами), за теоремою косинусів запишемо  де d – відстань між дротами. Звідси
де d – відстань між дротами. Звідси
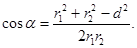
Після підстановки числових значень отримаємо

Підставляючи в формулу (2) значення вхідних величин, визначаємо шукану індукцію:

Приклад 2. Електрон, пройшовши прискорюючу різницю потенціалів U = 400 В, потрапив в однорідне магнітне поле напруженістю Н = 103 А/м. Визначити радіус R кривизни траєкторії і частоту n обертання електрону в магнітному полі. Вектор швидкості перпендикулярний до ліній поля.
Розв’язок. Радіус кривизни траєкторії електрона визначимо, виходячи з наступних міркувань: на електрон, що рухається в магнітному полі, діє сила Лоренца 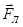 (дією сили тяжіння можна знехтувати). Сила Лоренца перпендикулярна вектору швидкості, отже, вона надає електрону нормальне прискорення. За другим законом Ньютона можна записати FЛ = man, де an – нормальне прискорення або
(дією сили тяжіння можна знехтувати). Сила Лоренца перпендикулярна вектору швидкості, отже, вона надає електрону нормальне прискорення. За другим законом Ньютона можна записати FЛ = man, де an – нормальне прискорення або
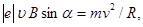 (1)
(1)
де е – заряд електрону;
υ – швидкість електрона;
В – магнітна індукція;
m – маса електрона;
R – радіус кривизни траєкторії;
a – кут між напрямком вектора швидкості 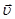 і вектором
і вектором  (в даному випадку
(в даному випадку 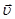 ^
^  і a = 900, sin a = 1).
і a = 900, sin a = 1).
З формули (1) знайдемо
 (2)
(2)
Імпульс mυ, що входить в рівняння (2) може бути виражений через кінетичну енергію Т електрона:
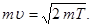 (3)
(3)
Але кінетична енергія електрона, що пройшов прискорюючу різницю потенціалів U, визначається рівнянням
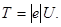
Підставивши цей вираз Т в формулу (3), отримаємо
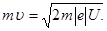
Магнітна індукція В може бути виражена через напруженість Н магнітного поля в вакуумі:
В = m0 Н,
де m0 – магнітна стала.
Підставивши знайдені вирази В і mυ в формулу (2), визначимо
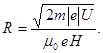 (4)
(4)
Виразимо всі величини, що входять в формулу (4), в одиницях СІ: m = 9,11 × 10-31 кг (із довідкової таблиці 17),  = 1,60 × 10-19 Кл, U = 400 В, m0 = 4p × 10-7 Гн/м, Н = 103 А/м. Підставимо ці значення в формулу (4) і обчислимо:
= 1,60 × 10-19 Кл, U = 400 В, m0 = 4p × 10-7 Гн/м, Н = 103 А/м. Підставимо ці значення в формулу (4) і обчислимо:
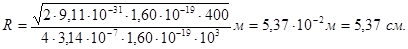
Для визначення частоти обертання n скористаємось формулою, що зв’язує частоту зі швидкістю і радіусом:
n = υ / 2p R. (5)
Підставивши в формулу (5) вираз (2) для радіуса кривизни, отримаємо
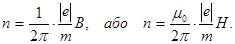
Всі величини, що входять в цю формулу, раніше були виражені в одиницях СІ. Підставимо їх і проведемо обчислення:
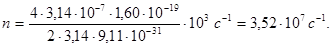
Приклад 3. Від двох когерентних джерел S1 та S2 (l = 0,8 мкм) промені падають на екран. На екрані спостерігається інтерференційна картина. Коли на шляху одного з променів перпендикулярно до нього помістили мильну плівку (n = 1,33), інтерференційна картина змінилась на протилежну. При якій найменшій товщині dmin плівки це можливо?
Розв’язок. Зміна інтерференційної картини на протилежну означає, що та тих ділянках екрана, де спостерігались інтерференційні максимуми, стали спостерігатися інтерференційні мінімуми. Така зміна інтерференційної картини можлива при зміні оптичної різниці ходу променів на непарне число половин довжин хвиль, тобто,
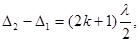 (1)
(1)
де D1 – оптична різниця руху променів до внесення плівки;
D2 – оптична різниця ходу тих самих променів після внесення плівки;
k = 0, ± 1, ± 2,....
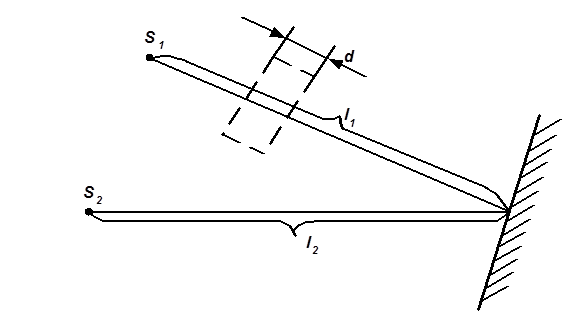
Рисунок 2.
Найменша товщина dmin плівки відповідає k = 0. При цьому формула (1) буде мати вид
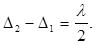 (2)
(2)
Виразимо оптичні різниці ходу D2 та D1. Із рис. 2 виходить:
D1 = l1 – l2,
D2 = [(l1 – dmin) + ndmin] – l2 = (l1 – l2) + dmin (n – 1).
Підставимо вирази D2 та D1 в формулу (2):
(l1 – l2) + dmin (n – 1) - (l1 – l2) = 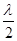 ,
,
або
dmin (n – 1) = 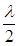 .
.
Звідси
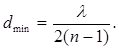
Підставивши числові значення, знайдемо

Приклад 4. На дифракційну гратку у напрямку нормалі до її поверхні падає монохроматичне світло. Період гратки d = 2 мкм. Якого найбільшого порядку дифракційного максимуму надає ця гратка у випадку червоного (l1 = 0,7 мкм) та у випадку фіолетового (l2 = 0,41 мкм) світла?
Розв’язок. На підставі відомої формули дифракційної гратки запишемо вираз порядку дифракційного максимуму:
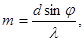 (1)
(1)
де d – період гратки;
j - кут між напрямком на дифракційний максимум і нормаллю до гратки;
l - довжина хвилі монохроматичного світла.
Так як sin j не може бути більшим за 1, то, як це слідує з формули (1), число m не може бути більшим d / l, тобто
m £ d / l. (2)
Підставивши у формулу (2) числові значення, знайдемо:
для червоних променів m £ 2 / 0,7 = 2,86;
для фіолетових променів m £ 2 / 0,41 = 4,88.
Якщо враховувати, що порядок максимумів є цілим числом, то для червоного світла mmax = 2 і для фіолетового mmax = 4.
Приклад 5. Природній промінь світла падає на поліровану поверхню скляної пластини, яка розміщена в рідині. Відбитий від пластини промінь світла утворює кут j = 970 з променем, який падає (рис. 3) Визначити показник заломлення n1 рідини, якщо відбитий промінь світла максимально поляризований.
Розв’язок. Згідно закону Брюстера, промінь світла, відбитий від діелектрика, максимально поляризований в тому випадку, якщо тангенс кута падіння чисельно дорівнює відносному показнику заломлення: tg i1 = n21, де n21 – показник заломлення другого середовища (скла) відносно першого (рідини).
Відносний показник заломлення дорівнює відношенню абсолютних показників заломлення. Отже, tg i1 = n2 / n1.
Так як кут падіння дорівнює куту відбиття, то і1 = j / 2 і, tg j / 2 = n2 / n1 звідки

Підставивши числові значення, знайдемо
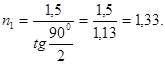

Рисунок 3.
Приклад 6. Два ніколі N1 і N2 розташовані так, що кут між їхніми площинами пропускання a = 600. Визначити, у скільки разів зменшиться інтенсивність l0 природного світла: 1) при проходженні через один ніколь N1; 2) при проходженні через обидва ніколі. Коефіцієнт поглинання світла в ніколі k = 0,05. Втрати на відбиття світла не враховувати.
Розв’язок. Природне світло, яке падає на грань призми ніколя (рис. 4) розщеплюється внаслідок подвійного променезаломлення на два промені: звичайний та незвичайний. Обидва промені однакові за інтенсивностями і повністю поляризовані. Площина коливань незвичайного променя лежить в площині креслення (площина головного перерізу). Площина коливань звичайного променя перпендикулярна площині креслення. Звичайний промінь о внаслідок повного внутрішнього відбиття від межі АВ відбивається на зачорнену поверхню призми і поглинається нею. Незвичайний промінь е проходить крізь призму, зменшуючи свою інтенсивність внаслідок поглинання. Таким чином, інтенсивність світла, яке пройшло крізь першу призму,
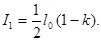
Відносне зменшення інтенсивності світла одержимо, поділивши інтенсивність l0 природного світла, яке падає на перший ніколь, на інтенсивність l1 поляризованого світла:
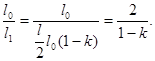 (1)
(1)
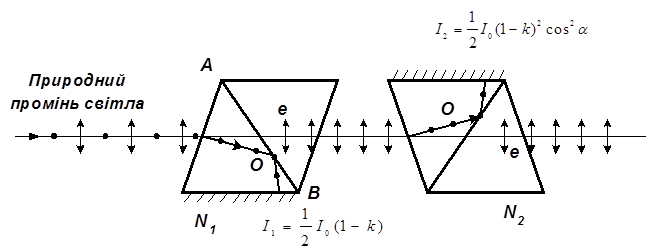
Рисунок 4.
Підставивши в (1) числові значення, знайдемо
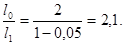
Таким чином, інтенсивність зменшиться в 2,1 рази.
2. Плоскополяризований промінь світла інтенсивності l1 падає на другий ніколь N2 і також розщеплюється на два промені різної інтенсивності: звичайний та незвичайний. Звичайний промінь повністю поглинається призмою, тому інтенсивність його нас не цікавить. Інтенсивність незвичайного променя l2, який вийшов з призми N2, визначається законом Малюса (без урахування поглинання світла у другому ніколі):
l2 = l1 cos2a,
де a – кут між площиною коливань в поляризованому проміні і площиною пропускання
ніколя N2.
Враховуючи втрати інтенсивності на поглинання в другому ніколі, одержимо
l2 = l1 (1 – k) cos2a.
Шукане зменшення інтенсивності при проходженні світла через обидва ніколі знайдемо, поділивши інтенсивність l0 природного світла на інтенсивність l2 світла, яке пройшло систему із двох ніколей:

Замінивши відношення l0 / l1 його виразом по формулі (1), одержимо
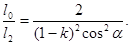
Підставивши дані, проведемо обчислення:
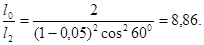
Таким чином, після проходження світла крізь два ніколі інтенсивність його зменшиться в 8,86 рази.
Приклад 7. Довжина хвилі, на яку припадає максимум енергії у спектрі випромінювання абсолютно чорного тіла, l0 = 0,58 мкм. Визначити енергетичну світимість (випромінюваність) Re поверхні тіла.
Рішення. Енергетична світимість Re абсолютно чорного тіла у відповідності з законом Стефана-Больцмана пропорційна четвертому ступеню абсолютної температури і виражається формулою
Re = sT4, (1)
де s – постійна Стефана-Больцмана;
Т – термодинамічна температура.
Температуру Т можна обчислити за допомогою закону зміщення Віна
l0 = b / T, (2)
де b – постійна закону зміщення Віна.
Використовуючи формули (2) і (1) одержимо
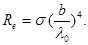 (3)
(3)
Випишемо числові значення величин, які містяться в цій формулі:
s = 5,67 × 10-8 Вт/(м2×К4), b = 2,90 × 10-3 м×К, l0 = 5,8 × 10-7 м, і підставивши числові значення в формулу (3), проведемо обчислення:
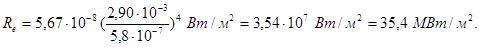
Приклад 8. Визначити максимальну швидкість υmax фотоелектронів, які вириваються з поверхні срібла: 1) ультрафіолетовими променями з довжиною хвилі l1 = 0,155 мкм; 2) g -променями з довжиною хвилі l2 = 1 пм.
Розв’язок. Максимальну швидкість фотоелектронів можна визначити з рівняння Ейнштейна для фотоефекта
e = А + Тmax, (1)
де e – енергія фотонів, які падають на поверхню металу;
А – робота виходу;
Тmax, - максимальна кінетична енергія фотоелектронів.
Енергія фотона обчислюється також за формулою
e = hc / l, (2)
де h – постійна Планка;
с – швидкість світла у вакуумі;
l – довжина хвилі.
Кінетична енергія електрона може бути виражена або класичною формулою
 (3)
(3)
або релятивістською
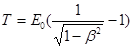 , (4)
, (4)
в залежності від того, яка швидкість надається фотоелектрону. Швидкість фотоелектрона залежить від енергії фотона, який спричиняє фотоефект: якщо енергія e фотона набагато менша за енергію спокою Е0 електрона, то можна застосувати формулу (3), якщо ж e зрівнянна за величиною з Е0, то обчислення за формулою (3) приведе до помилки, тому треба скористатися формулою (4).
1. Обчислимо енергію фотона ультрафіолетових променів за формулою (2):
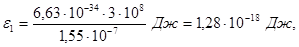
або
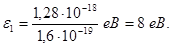
Одержана енергія фотона (8 еВ) набагато менша за енергію спокою електрона (0,51 МеВ). Отже, для даного випадку кінетична енергія фотоелектрона у формулі (1) може бути виражена класичною формулою (3):

звідки
 (5)
(5)
Випишемо числові значення величин: e1 = 1,28 × 10-18 Дж (обчислено вище), А = 4,7 еВ = 4,7 × 1,6 × 10-19 Дж = 0,75 × 10-18 Дж, m0 = 9,11 × 10-31 кг.
Підставивши числові значення у формулу (5) знайдемо
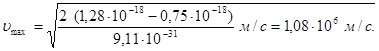
2. Обчислимо енергію фотона g -променів:
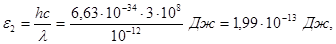
або

Робота виходу електрона (А = 4,7 еВ) мала у порівнянні з енергією фотона (e2 = 1,24 МеВ), тому можна прийняти що максимальна кінетична енергія електрона дорівнює енергії фотона: Тmax = e2 = 1,24 МеВ. Так як у даному випадку кінетична енергія електрона більша його енергії спокою, то для обчислення швидкості електрона слід взяти релятивістську формулу кінетичної енергії (4). З цієї формули знайдемо

Помітивши, що υ = cb i Tmax = e2 одержимо
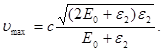
Підставимо числові значення величин і обчислимо:
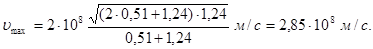
Приклад 9. Електрон в атомі водню перейшов з четвертого енергетичного рівня на другий. Визначити енергію випущеного при цьому фотона.
Розв’язок. Для визначення енергії фотона скористаємося серійною формулою для воднеподібних іонів:
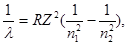 (1)
(1)
де l – довжина хвилі фотона;
R – постійна Ридберга;
Z – заряд ядра у відносних одиницях (при Z = 1 формула переходить в серійну формулу
для водню);
n1 – номер орбіти, на яку перейшов електрон;
n2 – номер орбіти, з якої пішов електрон (n1 і n2 – головні квантові числа).
Енергія фотона e виражається формулою
e = hc / l.
Тому, помноживши обидві частини рівняння (1) на hc, одержимо вираз для енергії фотона

Так як величина Rhc є енергія іонізації Еі атому водню, то
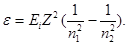
Обчислення виконаємо у позасистемних одиницях: Еі = 13,6 еВ; Z = 1 (заряд ядра атому водню у відносних одиницях, де за одиницю заряду прийнято абсолютне значення заряду електрона); n1 = 2; n2 = 4;
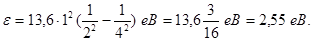
Приклад 10. Хвильова функція 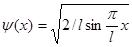 описує основний стан частки в нескінченно глибокій прямокутній потенційній ямі шириною l. Обчислимо ймовірність знаходження частки в малому інтервалі Dl = 0,01 l у двох випадках: 1) поблизу стінки (0 £ х £ D l); 2) в середній частині ями
описує основний стан частки в нескінченно глибокій прямокутній потенційній ямі шириною l. Обчислимо ймовірність знаходження частки в малому інтервалі Dl = 0,01 l у двох випадках: 1) поблизу стінки (0 £ х £ D l); 2) в середній частині ями 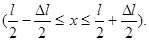
Розв’язок. Ймовірність того, що частка буде виявлена в інтервалі dx (від x до x + dx), пропорційна цьому інтервалу і квадрату модуля хвильової функції, яка описує даний стан, дорівнює
dw = ïy (x)ï2 dx.
У першому випадку шукана ймовірність знаходиться інтегруванням в межах від 0 до 0,01l (рис. 5):
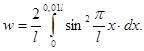 (1)
(1)

Рисунок 5.
Позначка модуля опущена, так як y -функція у даному випадку не є комплексною.
Так як х змінюється в інтервалі 0 £ х £ 0,01l і, отже  , правильне приблизне рівняння
, правильне приблизне рівняння
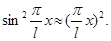
З урахуванням цього вираз (1) буде мати вид
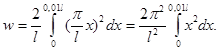
Після інтегрування одержимо
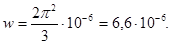
У другому випадку можна обійтися без інтегрування, так як квадрат модуля хвильової функції поблизу її максимуму в заданому малому інтервалі (Dl = 0,01l) практично не зміниться. Шукана ймовірність у другому випадку визначається виразом
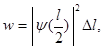
або

Приклад 11. Обчислити дефект маси і енергію зв’язку ядра 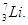
Розв’язок. Маса ядра завжди менша суми мас вільних (поза ядром) протонів і нейтронів, із яких ядро складається. Дефект маси ядра Dm і є різниця між сумою мас вільних нуклонів (протонів і нейтронів) і масою ядра, тобто
Dm = Zmp + (A – Z) mn – m, (1)
де Z – атомний номер (число протонів у ядрі);
A – масове число (число нуклонів);
mр, mn, m – відповідно маси протона, нейтрона і ядра.
В довідкових таблицях завжди даються маси нейтральних атомів, але не ядер, тому формулу (1) доцільно перетворити так, щоб в неї входила маса М нейтрального атома. Можна враховувати, що маса нейтрального атома дорівнює сумі мас ядра і електронів, які складають електронну оболонку атома:
М = m + Zme,
звідки
m = M – Zme.
Виразивши в рівнянні (1) масу ядра за останньою формулою, одержимо
Dm = Zmp + (A – Z) mn – M + Zme,
або
Dm = Z (mp + mn) + (A – Z) mn – M.
Помітивши, що mp + mn = МН, де МН – маса атома водню, остаточно одержимо
Dm = ZМН + (A – Z) mn – M. (2)
Підставивши у вираз (2) числові значення мас (із довідкових таблиць), одержимо
Dm = [3× 1,00783 + (7 – 3) × 1,00867 – 7 × 0,1601] а.е.м. = 0,04216 а.е.м.
Енергією зв’язку DЕ ядра називається енергія, яка в тій чи іншій формі виділяється при створенні ядра з вільних нуклонів.
У відповідності з законом пропорційності маси і енергії
Е = с2Dm, (3)
де с – швидкість світла у вакуумі.
Коефіцієнт пропорційності с2 може бути виражений двояко:
с2 = 9 × 1016 м2/с2
або
с2 = DЕ /Dm = 9 × 1016 Дж/кг.
Якщо обчислити енергію зв’язку, користуючись позасистемними одиницями, то с2 = 931 МеВ/а.е.м. З урахуванням цього формула (3) буде мати вид
Е = 931 Dm (МеВ). (4)
Підставивши раніше знайдене значення дефекту маси ядра у формулу (4), одержимо
Е = 931 × 0,04216 МеВ = 39,2 МеВ
Примітка. Термін “дефект маси” іноді застосовують у другому значенні: дефектом маси D називають різницю між масою нейтрального атому М даного ізотопу і його масовим числом: D = М – А. Ця величина особливого фізичного сенсу не має, але її використання дозволяє у ряді випадків значно спростити обчислення. У цьому посібнику всюди мається на увазі дефект маси Dm, який визначається формулою (1).
Приклад 12. При зіткненні a -частки з ядром бора 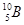 сталася ядерна реакція, в результаті якої створилося два нових ядра. Одним з цих ядер було ядро атома водню
сталася ядерна реакція, в результаті якої створилося два нових ядра. Одним з цих ядер було ядро атома водню 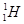 . Визначити порядковий номер і масове число другого ядра, дати символічний запис ядерної реакції і визначити її енергетичний ефект.
. Визначити порядковий номер і масове число другого ядра, дати символічний запис ядерної реакції і визначити її енергетичний ефект.
Розв’язок. Позначимо невідоме ядро символом  . Так як a -частка є ядром гелію
. Так як a -частка є ядром гелію 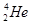 , запис реакції буде мати вид
, запис реакції буде мати вид

Скориставшись законом збереження числа нуклонів, отримаємо рівняння
4 + 10 = 1 + А, звідки А = 13.
На підставі закону збереження заряду, отримаємо рівняння
2 + 5 = 1 + Z,
звідки Z = 6.
Отже, невідоме ядро є ядром атома ізотопу вуглецю 
Тепер можемо записати реакцію в остаточному виді:
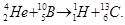
Енергетичний ефект Q ядерної реакції визначається за формулою
Q = 931 [(mHe + mB) – (mH + mC)].
Тут в перших круглих дужках зазначені маси вихідних ядер, у других дужках – маси ядер – продуктів реакції. При числових розрахунках за цією формулою маси ядер замінюють масами нейтральних атомів. Можливість такої заміни виходить з наступних міркувань.
Число електронів в електронній оболонці нейтрального атома дорівнює його зарядовому числу Z. Сума зарядових чисел вихідних ядер дорівнює сумі зарядових чисел ядер – продуктів реакції. Отже, електронні оболонки ядер гелію і бору містять разом стільки ж електронів, скільки їх містять електронні оболонки ядер вуглеводу і водню.
Очевидно, що при відніманні суми мас нейтральних атомів вуглецю і водню із суми мас атомів гелію і бору маси електронів випадуть і ми отримаємо той самий результат, коли б брали маси ядер. Підставивши маси атомів, взяті із довідкової таблиці, в розрахункову формулу, одержимо
Q = 931[(4,00260 + 10,01294) – (1,00783 + 13,00335)] МеВ = 4,06 МеВ.
Приклад 13. Визначити початкову активність радіоактивного препарату магнію 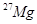 масою m = 0,2 мкг, а також його активність А протягом часу t = 6 год. Період напіврозпаду Т1/2 магнію рахувати відомим.
масою m = 0,2 мкг, а також його активність А протягом часу t = 6 год. Період напіврозпаду Т1/2 магнію рахувати відомим.
Розв’язок. Активність А ізотопу характеризує швидкість радіоактивного розпаду і дорівнює числу ядер, які розпадаються за одиницю часу:
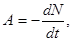
де dN – число ядер, які розпадаються за час dt.
Згідно основного закону радіоактивного розпаду 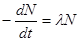 , де l - постійна радіоактивного розпаду. Так як N = N0 e-lt, де N0 – число ядер, які не розпалися, на момент часу, прийнятий за початковий, то
, де l - постійна радіоактивного розпаду. Так як N = N0 e-lt, де N0 – число ядер, які не розпалися, на момент часу, прийнятий за початковий, то
А = l N0 e-lt.
Очевидно, що початкова активність (при t = 0)
А0 =lN0. (1)
Тому закон зміни активності з часом виражається формулою
А = А0 е-lt. (2)
Початкову активність визначимо за формулою (1). Постійна радіоактивного розпаду l, яка входить до цієї формули, може бути виражена через період напіврозпаду співвідношенням l = Іn 2/T1/2 = 0,693 / T1/2. Для 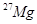 період напіврозпаду Т1/2 = 10 хв. = 600 сек. Отже,
період напіврозпаду Т1/2 = 10 хв. = 600 сек. Отже,
l = 0,693 / 600 с-1 = 1,15 × 10-3 с-1.
Число радіоактивних атомів N0, які містяться в ізотопі, дорівнює добутку числа Авогадро NА на кількість речовини n даного ізотопу:

де m – маса ізотопу;
m - молярна маса.
Виразивши в цій формулі значення величин в одиницях СІ, одержимо
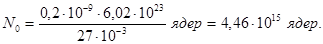
Розрахуємо за формулою (1) початкову активність ізотопу:
А0 = lN0 = 1,15 × 10-3 × 4,46 × 1015 Бк = 5,13 × 1012 Бк,
або
А0 = 5,13 ТБк.
Активність через 6 годин (6 год = 2,16 × 104 с) одержимо за формулою (2):
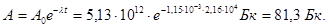
Date: 2015-11-15; view: 849; Нарушение авторских прав