Остатки регрессии, шумы и катастрофы

Оценки параметров регрессии должны отвечать определенным критериям:

- несмещенность оценки (такое состояние оценок при котором математическое ожидание остатков равно нулю);

- эффективность (оценки при которых остатки регрессии имеют наименьшую дисперсию);

- состоятельность (такое значение оценок при котором увеличение объёма выборки ведет к увеличению точности оценок).

Согласно теории эконометрического анализа следует проводить исследование остатков регрессии на наличие следующих пяти предпосылок метода наименьших квадратов:

- случайный характер остатков;

- нулевая средняя величина остатков, не зависящая от номера наблюдения;

- гомоскедастичность (дисперсия отклонений одинакова для любого интервала наблюдений);

- отсутствие автокорреляции в остатках;

- нормальный характер распределения остатков по величине и направлению.

Прежде всего, проверяется случайный характер остатков - первая предпосылка МНК.

С этой целью строится график зависимости остатков от теоретических значений результативного признака.

Если на графике получена горизонтальная полоса (в соответствии с рисунком 6), то остатки представляют собой случайные величины и МНК оправдан, теоретические значения аппроксимируют фактические значения наблюдаемой величины.

Рисунок 6 - Остатки регрессии

Возможны следующие случаи: если остатки регрессии зависит от прогнозного значения, это может наблюдаться в следующих случаях:

- остатки не случайны (в соответствии с рисунком 7);

Рисунок 7 - Остатки регрессии не случайны

- остатки не имеют постоянной дисперсии(в соответствии с рисунком 8);

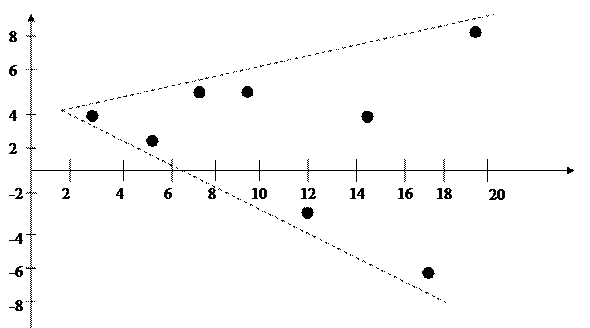
Рисунок 8 - Остатки регрессии с возрастающей дисперсией

- остатки носят систематический характер(в соответствии с рисунком 9).

Рисунок 9 - Систематический характер остатков регрессии

Для оценки гетероскедастичности может использоваться метод Гольдфельда-Квандта.

Алгоритм метода Гольдфельда-Квандта.

1 Упорядочить выборку из n элементов по мере возрастания наблюдаемой переменной.

2 Исключить из рассмотрения некоторое количество наблюдений (k) взятых из середины выборки, при этом соблюдать соотношение (38).

(n-k)/2>p (38)

где p - число оцениваемых параметров.

3 Разделение оставшейся выборки на две группы (до исключённого участка и после) с последующим определением по каждой из групп уравнения регрессии.

4 Определение остаточной суммы квадратов остатков регрессии для первой и второй выборки и нахождение их отношения.

5 При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F -критерию с: (n-C-2p):2 степенями свободы для каждой остаточной группы квадратов.

6 Чем больше величина превышает табличное значение F -критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.

При построении уравнения регрессии как правило объяснить удаётся динамику прогнозируемой величины не полностью, а лишь некоторую её часть, как следствие между прогнозируемой величиной и её фактическим значением есть некоторая разница - остатки регрессии. В идеальном случае они должны быть подчинены закону нормального распределения - тогда их можно списать на случайные колебания, но это не всегда так.

При достаточно большом количестве наблюдений распределение остатков регрессии не принимают во внимание, а оценки параметров регрессии найденные методом наименьших квадратов считают несмещёнными.

Отклонение остатков регрессии от нормального закона распределения может свидетельствовать как о неучтённых в уравнении регрессии переменных оказывающих влияние на оцениваемую величину так и о характере процесса.

При реализации методов эконофизики необъяснённые при прогнозировании остатки рассматривают как различные шумы, наибольшее информативное значение имеет своевременное опознание чёрного шума - шума катастроф.

Если случайные колебания параметра подходят под описание чёрного шума следует ожидать такое наложение случайных колебаний друг на друга при котором возможно резкое кратковременное увеличение амплитуды с возможным, но не обязательным, резким изменением среднего уровня.

Чёрный шум описывается формулой (39) [48]

1/ω ^β, β > 2 (39)

Анализ рядов динамики интерпретирующий колебания как шумы опирается на оценку спектра мощности (квадрат амплитуды преобразования Фурье) S(ω) относительных частот интервалов ω. В общем случае такая зависимость может быть аппроксимирована соотношением (40)

S(ω) ≈ c ω^-β (40)

где с - константа, параметр;

β - некоторый показатель спада функции S.

Прологарифмируем обе части уравнения и получим (41).

ln S(ω) = c - β ln ω (41)

Следовательно если изобразить графически наклон сглаженных спектров в зависимости от показателя β (в соответствии с рисунком 10).

Если β = 0, то шум называется белым: спектр мощности не зависит от частоты, т.е. он в среднем не спадает. Спектр постоянный.

При β = 2 спектр будет пропорционален 1/ω² в широком диапазоне частот. Такой шум называется коричневым и его можно получить, если проинтегрировать белый шум один раз по времени, таким образом получив подобие проекции броуновского движения на одно пространственное измерение.

Между белым и коричневым находится шум со спектром 1/ω - розовый шум.

Если β>2, то шум - чёрный.

Рисунок 10 - Наклон сглаженных спектров при разных β

Преобразование Фурье для определения спектра мощности (квадрата амплитуды) может быть проведено с помощью простого алгоритма, реализованного на С++ (в соответствии с рисунком 11).

Рисунок 11 - Простой способ провести преобразование Фурье

Соответственно логике приведенного алгоритма для преобразования Фурье будет справедливо выражение(42).

(42)

где определяется через формулу (43) за исключением двух случаев (45, 46);

определяется через формулу (44).

(43)

(44)

(45)

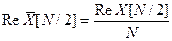(46)

Не сложно догадаться что формула (42) является обратным преобразованием Фурье.

Date: 2015-11-14; view: 511; Нарушение авторских прав