Фрактальные методы

Сторонники фрактальных методов пролагают свой путь от гипотезы эффективного рынка, согласно которой вся существующая информация немедленно и в полной мере отражается на цене к гипотезе фрактального рынка, согласно которой информация поступает к субъектам рыночных отношений в разное время, что порождает одинаковые реакции от разных субъектов рынка в разные временные моменты.

Неравномерность поступления информации и разнообразие реакций отражаются на рыночной динамики в виде визуальной схожести динамики цен за разные промежутки времени: за день, за неделю, за месяц... - что в свою очередь приводит к одинаковой доходности при ведении торгов на разных временных интервалах.

Дополнительным же аргументом в поддержку фрактальной гипотезы рынка служит сохранение значений фрактальных мер: показателя Хёрста, фрактальной размерности - при расчёте этих показателей на разных временных интервалах.

Показатель Херста в основе своей содержит формулу (22) из работы Альберта Эйнштеина о броуновском движении частиц.

(22)

где R - расстояние пройденное броуновской частицей за время T.

Изменение цены деления временной шкалы равно как и шкалы расстояния способно повлиять на формулу, чтобы избавится от такого влияния введем коэффициенты при переменных и выразим меру количества отклоняющихся значений переменной(23).

(23)

где R - размах накопленного отклонения от среднего;

S - среднеквадратическое отклонение ряда наблюдений;

α - длительность периода наблюдения;

N - количество периодов наблюдения;

H - показатель Хёрста.

Следуя этой логике при показателе Хёрста равном 0,5 - наблюдается случайное явление (Таблица 1).

Таблица 1 - Интерпритация показателя Хёрста

Значение показателя Хёрста	Интерпритация
Н = 0	Никаких движений или они цикличны с очень большой частотой колебаний
	Значение переменной стремится возвратиться к среднему значению
	Случайный характер наблюдаемого явления
	Ряд значений с высокой вероятностью случайный, при малом количестве наблюдений
	Трендоустойчивый (персистентный) рынок
	Значение показателя Хёрста для большинства природных явлений
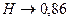
	Значение к которому стремится линейный тренд, при достаточно долгих периодах наблюдения
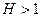
	Очень редкое явление. Независимые скачки амплитуды, распределенные по Леви

При проведении R/S анализа (расчёта показателя Хёрста) можно однозначно ответить влияют ли какие-либо силы на движение цены или же движение хаотично.

Размерность - количество независимых параметров, необходимых для описания состояния объекта, равно как и необходимое для указания на любую из его частей.

В рамках данной работы справедливо приравнивать к понятию степеней свободы, которые в свою очередь записываются в виде произведения символов соответствующих основным параметрам системы.

Размерность указывает сколько величин – координат нужно указать для однозначного определения каждого элемента множества.

С лёгкостью можно определить размерность простых геометрических фигур так привычных математикам. Так размерность точки равна нулю, линии – единице, квадрата – двум. В мире ещё много разных примеров так для описания сложных химических процессов может потребоваться указать температуру, физических – спектр волы и другие показатели…

В рамках данной работы целесообразно ограничится линейными параметрами при определении размерности.

Представим следующую задачу:

Необходимо определить размерность квадрата, а значит нужно учесть все элементы квадрата.

Наибольшая мера отличная от нуля для квадрата это площадь, для куба – объём. Степень, в которую мы возводим длину стороны объекта, показывает скольки мерным является объект. Положив в основу логики такое наблюдение не сложно написать формулу (24).

(24)

где М – наибольшая мера позволяющая учесть все элементы множества отличная от нуля;

a – линейный размер стороны объекта;

n – степень, показывающая размерность объекта.

Согласно этой формуле размерность можно найти в виде результата расчёта (25).

(25)

где М – все элементы множества, размерность которого вычисляется.

Таким образом: находится размерность множества (размерность Минковского) которую можно представить формулой (26).

(26)

где M-размерность Минковского;

– количество элементов;

- размер элемента.

Проверим приведенную формулу на нескольких примерах.

Квадрат можно представить в виде нескольких меньших квадратов со стороной кратной стороне первоначального квадрата (в соответствии с рисунком 3). При этом, чем меньше размер стороны малых квадратов, тем большее количество этих квадратов понадобится (Таблица 2).

Рисунок 3 - Квадрат и его деление

Таблица 2 - Соотношение стороны элемента и количеству элементов

Сторона малого квадрата, (от стороны большого квадрата)	Количество квадратов необходимое для полного покрытия, N
1/2*а
1/3*а
1/4*а

Не сложно выявить взаимосвязь этих величин описывается следующей формулой (27).

(27)

Подставим в формулу для определения размерности получим выражение (28)

(28)

И действительно, размерность квадрата равна 2.

Согласно приведенной логике размерность Минковского для отрезка может быть найдена в виде следующего (29).

(29)

Размерность отрезка согласно ожиданиям действительно равна единице.

Для восприятия всей глубины представленной формулы рассчитаем размерность множества Кантора (в соответствии с рисунком 4).

Множество Кантора представляет собой линию, поделенную на три разные части из которой убрали среднюю часть, с оставшимися двумя частями повторили то же действие неограниченное число раз.

Рисунок 4 - Канторово множество [75]

Для такого множества зависимость количество элементов необходимое для покрытия всего множества от их размера весьма сложно определить (Таблица 3).

Таблица 3 - Соотношение стороны элемента и количеству элементов

1/3
1/9
1/27

Таким образом зависимость количества элементов от их размера можно выразить формулой (30) или иначе (31).

(30)

(31)

Подставив выражение (31) в формулу размерности Минковского(26) получим результат 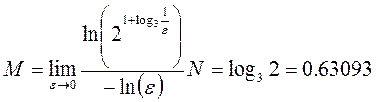(32):

(32)

Полученное значение несколько меньше единицы, ровно как и множество Кантора несколько меньше линии.

Согласно приведенной логике можно записать, что размерность такого множества рассчитывается по формуле (33): линия разделяется на 2 части с коэффициентом подобия 1/3.

(33)

Традиционным в рамках фрактальной теории становится использование размерности Хаусдорфа. Размерность Минковского в большинстве случаев совпадает с размерностью Хаусдорфа, превышая её лишь в некоторых случаях для абстрактных математических множеств.

Для анализа финансовых рынков использование таких методов определения размерности затруднительно, так как зависимость динамики цен заранее не установлена и нет возможности рассчитать отношение количества элементов к их размеру. Для определения фрактальной размерности графика тренда цен используют метод Грассберга-Прокаччиа.

Согласно утверждению Пуанкаре: любая динамическая система должна через некоторое время принимать состояние сколь угодно близкое к исходному [18], а согласно теореме Такенса [79, 80], наблюдения значений лишь одной переменной системы в достаточно долгий период времени достаточны для расчета значений корреляционного интеграла, а следовательно и фрактальной размерности.

По Такенсу, необходимо представить пространство вложения (или псевдофазовое пространство) с m-мерным вектором по значениям одной физической переменной, взятым со сдвигом τ (34).

(34)

Среднее время возврата τ – период цикла Пуанкаре, можно рассчитать по формуле предложенной Смолуховским [78] (35):

(35)

где P_k – вероятность возврата системы в исходное состояние за время kt, где k - количество интервалов времени, t - их длительность.

Рассматриваемый временной ряд значений, таким образом, преобразуется в m-мерную фигуру. Такая фигура называется восстановленным аттрактором и представляет собой непрерывную линию без самопересечений. Ближайшая аналогия из жизни – клубок ниток. В условиях, если исходный ряд данных стационарен, положительных результатов добиться будет легче.

Для более легкого восприятия рассмотрим аналогию. Допустим, что правило отображения исходного аттрактора: как некоторого образа системы (а биржевая торговля по своей сути является системой оценки конкретного объекта, стоимость замещения (восстановительная или стоимость создания) которого не может меняться быстрее, а следовательно процесс можно рассматривать как стационарный при учёте инфляционных колебаний - не что иное как проекция трехмерного объекта на линию.

Для простоты рассмотрим проекцию куба на линию (в соответствии с рисунком 5).

Каждая вершина куба спроецирована на прямую.

Таким образом если рассматривать данную прямую как координатную ось и знать последовательность точек, мы будем иметь временной ряд состоящий из точек вершин куба от A до H.

Точки которые в исходном объекте находились дальше друг от друга могут оказаться ближе после проекции, именно этот эффект и является ключом к разгадке.

Рисунок 5 - Проекция куба на линию

Задача анализа временного ряда цен на актив состоит в обратном проецированию действии. Восстановить n-мерную фигуру, которая как правило не является кубом, c целью использования её формы как ориентира - аналога математического ожидания.

Форма может быть более чем трёхмерным объектом, что в свою очередь затрудняет отображение на плоскости. К счастью компьютерное моделирование не исключает возможности моделирования более чем 3-х мерных пространств.

Восстанавливаемая форма называется аттрактором.

аттрактор - компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности [76].

Аттрактор динамической системы при таком подходе в общем случае должен выглядеть как непрерывная n-мерная линия, сколь угодно близко приближающаяся к своей траектории, но без самопересечений.

Эти условия выполняются при отображении восстановленного аттрактора в пространство размерности не меньшей чем размерность исходного аттрактора.

Далее для каждого аттрактора рассчитывается корреляционный интеграл согласно формуле (36).

(36)

где N – количество точек аттрактора;

- абсолютное расстояние между i -ой и j -ой точками аттрактора в m – мерном пространстве;

- размер разрешающей ячейки;

- функция Хевисайда ( =0 при и =1 при ).

Таким образом, - оценка количества пар точек аттрактора расположенными в пределах заданного расстояния, отнесенная к полному количеству пар точек (оценка среднего количества близкорасположенных точек).

Согласно общей идеи расчета фрактальной размерности – как оценки скорости роста элементов с уменьшением наблюдаемой ячейки (37):

(37)

где – количество элементов.

Следует отобразить зависимость от в двойном логарифмическом масштабе.

Сопоставив линейным участкам функции прямые можно найти значение их производной, при этом для различных m значение производной будет меняться, но если графически изобразить зависимость значений производной от значений m то будет явно виден момент насыщения. Значение m в точке насыщения и есть искомая размерность пространства для восстанавливаемого аттрактора, а значение производной будет являться фрактальной размерностью Хаусдорфа-Безиковича, что легко доказывается при рассмотрении спектра Реньи [43].

Согласно теореме Такенса, эти характеристики отражают соответствующие значения динамической системы, породившей исследуемый ряд.

Так как фрактальная размерность, полученная таким образом, характеризует максимальную скорость изменения системы (найден максимум первой производной), можно дать следующую экономическую интерпретацию: что при наступлении определенного события (наступившего в критический момент времени, когда производная достигла максимума) максимальное количество участники рынка отреагировали на такое событие, но каждый из них отреагировал индивидуально, что повлекло максимальное количество проявлений реакций и даёт нам повод заключить мнение о конкретном числе выявленных экономико-психологически типов среди участников торгов. При таком рассмотрении становится ясно, что рассмотрение биржи как столкновения «быков» и «медведей» крайнеукрупнённое, что является недопустимым для профессионального участника торгов, более того меняя размеры разрешеющей ячейки в прямой зависимости к ожидаемым результатам (величины производимого прогноза) можно добиться оптимальной детализации количества возможных реакций.

При этом возможны две благоприятных ситуации: предсказуемость поведения графика при показателе размерности, стремящемся к единице (прямая линия нечего прогнозировать всё и так ясно, интерес консервативных инвесторов) и предсказуемость поведения графика при большом количестве равносильных реализуемых на бирже стратегий участников торгов.

Date: 2015-11-14; view: 749; Нарушение авторских прав