Эконометрический и статистический анализ

Первые попытки количественных исследований в экономике относятся к 17 веку. «Политические арифметики» — В. Пегги (1623-1667), Г. Кинг (1648-1712), Ч. Давенант (1656—1714) — вот первые ученые, систематически использовавшие цифры и факты в своих работах, в первую очередь в расчете национального дохода. Спектр их интересов был связан, как правило, с практическими вопросами: финансами, денежным обращением, налогообложением, торговлей и т.д.

Одним из первых был сформулирован «закон Кинга». В нем на основе соотношения между урожаем зерновых и ценами на зерно была выявлена закономерность спроса. Ученые хотели достичь в экономике того, что И. Ньютон достиг в физике. Еще не была определена неопределенная природа экономических закономерностей. В этот период все больше данных становятся доступными, создавая основу для исследований.

Существенным толчком стало развитие теории статистики в трудах Ф. Гальтона (1822-1911), Ф. Эджворта (1845—1926) и К. Пирсона (1857-1936). Появились первые применения парной корреляции: при выявлении связи между уровнем бедности и формами помощи бедным (Дж. Э. Юл,. 1895, 1896); между уровнем браков в Великобритании и благосостоянием людей (Г. Хукер, 1901), в котором было использовано несколько индикаторов благосостояния. Также исследовались временные ряды экономических данных. Это были первые шаги по созданию современной науки эконометрики.

Вместе с развитием эконометрики происходил процесс создания маржиналистской теории, зарождение которой можно отнести к 60-м годами XIX в. (работы Джевонса, Вальраса, Менгера). С 30-х годов 19 века страны с наибольшим уровнем развития капитализма стали испытывать упадок деловой активности и возникновение массовой безработицы. Эти явления не находили объяснения с точки зрения теории. Быстрая индустриализация выявила большой спектр социальных проблем, которые тоже не согласовывались с теорией. Неоклассическая теория стала восприниматься как слишком далекая от реальности. Для ее практического значения потребовались количественные выражения базовых понятий, таких как «предельная полезность» или «эластичность спроса».

Многие ученые признают первой работой, которую можно бы быть названа эконометрической, книгу американского экономиста Г. Мура (1869-1958) «Законы заработной платы: эссе по статистической экономике» (1911 год). Г. Муром был проведен анализ рынка труда, статистическая проверка теории производительности Дж. Кларка, были описаны основы стратегии объединения пролетариата и т. д. В это время для США решение этих вопросов было очень важным. Мур подошел к анализу этих проблем с позиций «высшей» статистики, используя все достижения теории корреляции, регрессии, анализа динамических (временных) рядов. Он хотел доказать, что сложные математические расчеты, наполненные фактическими данными, могли стать основой для разработки социальной стратегии.

К концу 19 века относится первое применение итальянским ученым Р. Бенини (1862—1956) модели множественной регрессии для оценки функции спроса. Существенным вкладом в становление эконометрики как науки явились работы по цикличности экономики. Французский физик К. Жюгляр (1819—1905), ставший экономистом, первым стал исследовать экономические временные ряды с целью выделения бизнес-циклов. Он получил цикличность инвестиций (продолжительность цикла — 7—11 лет). После Жюляра С. Китчин, С. Кузнец, Н. Кондратьев, по отдельности, выявили цикличность обновления оборотных средств (3-5 лет), цикличность в строительстве (15—20 лет), долгосрочные волны («большие циклы») Кондратьева, продолжительностью 45-60 лет.

Важным событием в формировании эконометрики стало построение экономических барометров, в первую очередь так называемого гарвардского барометра. Большинство экономических барометров, основано на следующем: в динамике разных показатели экономики существуют такие, которые в своих изменениях стоят впереди других, а потому могут служить предвестниками последних.

Гарвардский барометр был создан под руководством У. Персонса (1878—1937) и У. Митчелла (1874—1948). В течение 1903—1914 гг. он включал пять групп показателей, которые потом были сведены в три отдельные кривые: кривая А означала фондовый рынок; кривая В — товарный рынок; кривая С — денежный рынок. Каждая из этих кривых представляла собой среднюю арифметическую из рядов входящих в нее нескольких показателей. Эти ряды изначально статистически обрабатывались путем исключения тенденции, сезонной волны (сезонной компоненты).

В основу прогноза барометра полагалось свойство каждой отдельной кривой повторять движение остальных в определенной последовательности и с определенным отставанием. С 1903 г. до первой мировой войны повороты кривой А предшествовали поворотным пунктам кривой В на 6—10 месяцев; поворотные части кривой В опережали аналогичные пункты кривой С на 2—8 месяцев (в среднем на 4 мес.); колебания кривой С предшествовали колебания кривой А следующего цикла на 6—12 месяцев.

Гарвардский барометр описывал подмеченных эмпирических закономерностей и экстраполяции последних на последующие месяцы. Однако в построении гарвардского барометра существуют и некоторые теоретические предпосылки. Очевидно, что изменение средних биржевых курсов и показателей фондового рынка (индекс спекуляции А) означало изменение спроса на товары, что влечет за собой, изменение индекса оптовых цен, объема производства и товарооборота (индекс В). Увеличение объема производства вызывало напряжение на денежном рынке, рост учетной ставки и падение курса ценных бумаг с фиксированным доходом (кривая С). Максимум кривой А обычно должен совпадать с минимумом кривой С.

Успех гарвардского барометра породил буквально эпидемию в мире (в частности, аналогичный барометр был построен в Великобритании). Несколько лет после I мировой войны он еще выполнял свое предназначение. Но затем гарвардский барометр (с 1925 г.) потерял чувствительность и сошел на нет. Авторы гарвардского барометра объясняли его крах появлением мощного регулирующего фактора в экономике США. В этих условиях главным методом макроэкономического анализа становится метод «Затраты - выпуск» Леонтьева В.В.(1906-1999).

В СССР советский математик-статистик Е. Слуцкий (1880 - 1948) в своей работе «Сложение случайных причин как источник циклических процессов» (1927), взял в качестве случайных рядов последние цифры номеров облигаций из таблиц выигрышного займа, доказал, что «сложение случайных причин порождает волнообразные ряды, имеющие тенденцию на протяжении большего или меньшего числа волн имитировать гармонические ряды, сложенные из незначительного числа синусоид».

В 1912 г. И. Фишер пытается создать группу ученых для развития экономической теории путем ее связи со статистикой и математикой. Но в это время создать группу не получилось. Тогда Р. Фриш и математик-экономист Ч. Рус обратились с идеей созвать форум экономистов по вопросы взаимодействия экономики, статистики и математики.
29 декабря 1930 г. по инициативе И. Фишера (1867 - 1947), Р. Фриша, Я. Тинбергена (1903 - 1995) и других ученых на заседании Американской ассоциации развития науки в г.Кливленд создается эконометрическое общество, на котором норвежским ученый Р. Фришем новой науке дается название — «эконометрика».

Изначально общество было интернациональным. В 1950 г. эконометрическое общество насчитывало около 1000 ученых. С 1933 г. под редакцией Р. Фриша начинает издаваться журнал «Эконометрика» («Econometrica»), который и сейчас влияет на развитие эконометрической науки. В 1941 г. появляется первый учебник по эконометрике, созданный Я. Тинбергеном (1913 - 1994). В эти годы и до 70-х гг. XX в. эконометрика позиционировалась как эмпирическая оценка моделей, которые разработал экономической теорией. Р. Фриш определял соотношение между теорией и данными наблюдений таким образом: теория, абстрактно формулирующая количественные соотношения, должна быть подтверждена множеством наблюдений. Под влиянием лидеров, таких как Р. Фриш, Т. Хаавелмо, Я. Тинбергенг экономические модели были кейнсианскими.

Все меняется в 70-е гг. В макроэкономике возникают противоречия между кейнсианцами, монетаристами и марксистами. Формальные методы стали использовать для доказательства причинности при выборе теоретических концепций. Экономическая теория теряет свое главенствующее значение. Очень важным событием стало появление компьютеров с высокой мощностью. Развитие получил статистический анализ временных рядов. Г. Бокс и Г. Дженкинс создают ARIMA-модель в 1970 г., К. Симе и др. ученые - VAR-модели, ставшие популярными в начале 80-х гг. Пиком этой стадии развития явился метод коинтеграции, развитый С. Иохансеном и др. (1990 г.). На сегодняшний день эконометрика состоит из огромного количества моделей - от больших макроэкономических моделей, включающих сотни или даже тысячи уравнений, до малых коинтеграционных моделей, использующихся для решения специфических проблем [16].

Первым, что приходит на ум для целей прогнозирования динамики цен использовать мощь эконометрического аппарата - что позволяет строить прогнозы, а так же оценивать доходность и рискованность вложений в те или иные активы.

Длительное наблюдение за явлением имеющим вероятностную природу способно привести к закону распределения вероятностей наступления этого явления. Если обозначить итоги наступления такого события через переменную то можно представить закон распределения в виде сопоставления величины наблюдаемой переменной с вероятностью принятия переменной такого значения.

Так для монеты подброшенной вверх вероятность упасть решкой стремится к 0,5, то же касается и вероятности упасть орлом - тоже приблизительно в половине случаев, при всём при этом у монеты есть и другие варианты: упасть ребром или же не упасть совсем - которые с большинстве своём игнорируются исследователями в виду их крайней редкости.

При рассматривании некоторых системных явлений игнорирование в исследовании таких редких событий может быть не допустимо.

В основу многих методов положен нормальный закон или закон Гаусса распределения вероятностей (в соответствии с рисунком 1) который соответствует формуле 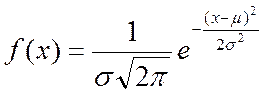(10)

(10)

где μ - математическое ожидание;

σ - стандартное отклонение.

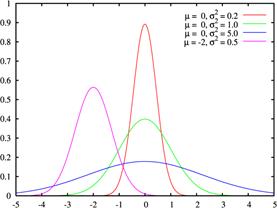
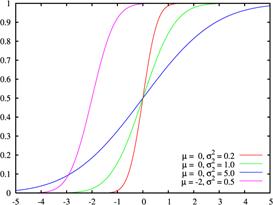
Рисунок 1 - Нормальное распределение [74]

Среднеквадратическое отклонение - это показатель рассеивания значений оцениваемой величины от её математического ожидания.

Математическое ожидание - значение, которое с наибольшей вероятностью примет исследуемая величина.

Такому распределению соответствуют такие величины как: расстояние от мишени до точки попадания лучника, ошибки измерений и пр.

Функция плотности вероятности с одним пиковым значением удобна прежде сего тем что минимизация величины среднеквадратического отклонения может позволить однозначно определить значение математического ожидания.

К сожаленью многие экономические процессы не подчиняются такому распределению. Для примера обратимся к закону распределения вероятностей построенному программой нормирования выработки рабочих сдельщиков (в соответствии с рисунком 2).

Применение в рассматриваемом случае метода наименьших квадратов было бы заведомо неверным.

Тем не менее эконометристы достигают значительных успехов в исследовании экономических процессов и их прогнозировании.

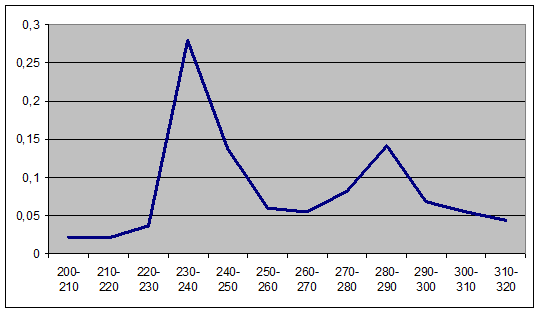
Рисунок 2 - Плотность вероятности принятия значений выработки рабочих

в разных интервалах на операции формования шлифовальных дисков завода «Росси»[62]

Рассмотрим этапы эконометрического исследования:

1 Постановка задачи (формулируется цель исследования, выполняется анализ предметной области) - теоретический этап.

2 Сбор данных и анализ их качества (информационный этап).

3 Формулировка модели (выбор спецификации).

4 Идентификация (определение, оценка) параметров модели.

5 Верификация (оценка качества модели).

6 Интерпретация результатов [72].

Сердцем такого подхода является эконометрическая модель, именно она позволяет прогнозировать будущие значения эндогенных переменных.

Ахиллесова пята же данного метода кроется в анализе качества исходных данных. Изначально предполагается, что прогнозируемый процесс подчиняется нормальному распределению - что даёт ряд весомых преимуществ в руки исследователя, одним из таких преимуществ выступает возможность использования метода наименьших квадратов.

Кроме того при использовании методов эконометрического анализа следует помнить об ограничениях на начальные данные, прежде всего в большинстве случаев анализируемый временной ряд должен являться стационарным - значения ряда должны быть одинаково распределены вне зависимости от сдвига времени, т.е. математическое ожидание, дисперсия и ковариация должны быть одинаковы для разных отрезков исследуемого ряда.

Большая часть критики направленной на эконометрические методы оперирует именно к несоответствию процессов нормальному закону распределения, что вообще-то сразу делает её несостоятельной в связи с тем что нарушение начальных условий построенной модели компрометирует исследователя её применявшего в такой ситуации, а не сам метод исследования.

Для достижения цели исследования учёные приверженцы методов эконометрики используют разные методы главным образом направленные на компенсирование выявленных слабых мест, так из не стационарных рядов данных вычитается возможный тренд или константа, при более сложных несоответствиях могут применяться специальные эконометрические поправки, такие как поправка Вайта.

Различные эконометрические модели устанавливают взаимосвязи между различными параметрами. Для целей прогнозирования могут быть полезны следующие модели: регрессионные модели, AR - модели, MA - модели, ARIMA - модели, ARCH и GARCH, GARP и GAP модели. Рассмотрим каждый вид модели подробнее.

Модель парной линейной регрессии устанавливает связь между двумя переменными. Уравнение парной линейной регрессии выглядит следующим образом 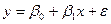(11):

(11)

где y - зависимая переменная;

x - независимая переменная;

ε - случайная компонента;

β₀ - константа;

β₁ - коэффициент регрессии.

Таким образом уравнение регрессии описывает взаимосвязь описываемой компоненты y, от значений принимаемых переменной x.

Построение уравнения парной линейной регрессии основывается на методе наименьших квадратов. Значения параметров β₀, β₁- подбираются таким образом, чтобы сумма квадратов отклонений прогноза от прогнозируемой величины была минимальна.

Множественная линейная регрессия отличается лишь количеством объясняющих переменных уравнение её описывающее можно записать в общем виде 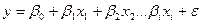(12).

(12)

Как и в первом случае отклонения между прогнозом и прогнозируемой величиной в идеальном случае должны соответствовать распределению Гаусса.

Нелинейные регрессионные модели очень разнообразны, наиболее пригодными для целей настоящего исследования являются модели с логарифмами, так как логарифмическая связь отражает затухание влияния фактора во времени, что может быть полезно при рассмотрении шоковых явлений в экономике.

AR - модели или авторегрессионные модели оценивают влияние значений прогнозируемой переменной которые она принимала в прошлые периоды времени на значения которые она принимает в будущем.

Уравнение регрессии (13) порядка p может быть обозначено как AR(p).

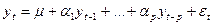(13)

где y_t - уровень ряда в текущий момент времени;

α_iy_t-i - влияние значения уровня ряда в момент времени i на текущее значение уровня ряда;

ε_t - остаток регрессии.

МА - модели или модели скользящей средней оценивают влияние остатков регрессии за прошлые временные интервалы на текущее значение уровня ряда.

При построении моделей такого вида следует помнить о том, что математическое ожидание остатков регрессии должно равняться 0, а распределение остатков регрессии должно быть подчинено нормальному закону распределения.

Уравнение регрессии в общем виде (14) будем называть процессом скользящей средней:

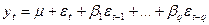(14)

где 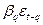- влияние остатка регрессии момента q на значение уровня ряда.

ARIMA - модели применяются в случае если уровень ряда не стационарен, а для приведения его к стационарному виду требуется его дифференцирование. Следует понимать последствия дифференцирования и верно интерпретировать полученную модель.

ARCH, GARCH и другие модели условной гетероскедастичности полагают что временной ряд является процессом описываемым следующим уравнением 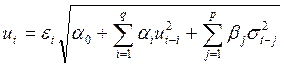(15)

(15)

где u_t - уровень ряда;

ε_t - белый шум;

α_i и β_j - параметры ряда;

q - порядок ARCH - членов исследуемого ряда;

p - порядок GARCH членов исследуемого ряда.

Математическое ожидание такого процесса равно нулю, дисперсия рассчитывается по формуле 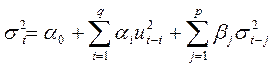(16)

(16)

В условиях стационарного процесса (17), дисперсия постоянна (18).

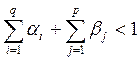(17)

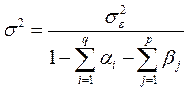(18)

Данный вид модели создан для учёта кластеризации волатильности.

Модели тренда и сезонности бывают двух видов: аддитивные (19) и мультипликативные (20).

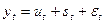(19)

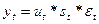(20)

где y_t - уровни временного ряда;

u_t - трендовая компонента;

s_t - сезонная компонента;

ε_t - случайная компонента.

Адаптивные методы прогнозирования представляют собой альтернативный подход к прогнозированию, в основе которого лежит допущение о том что изменение состояния системы происходит плавно, путём влияния на текущее значению некоторых факторов.

Адаптивных методов великое множество в основе этих методов всегда заключена логика описываемая формулой 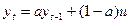(21)

(21)

где u - влияние фактора, чаще всего оценивается, как ошибка прогноза.

Возможны различные вариации приведенной формулы позволяющие учитывать сезонность, тренд и другие параметры, но метод уступает по своим возможностям регрессионному анализу.

Если рассматривать α, (1-α) - как значения коэффициентов регрессии мы получим частный случай MA модели, при этом коэффициенты будут зависимы и ограничены относительно друг друга, что исказит результаты. Применение такого метода оправдано лишь после аргументирования того факта, что сумма коэффициентов регрессии действительно близка к единице.

Date: 2015-11-14; view: 1161; Нарушение авторских прав