Закон сохранения импульса

Замкнутой (изолированной) системой тел называют такую систему, тела которой не взаимодействуют с внешними телами или если равнодействующая внешних сил равна нулю.

Если на систему материальных точек не действуют внешние силы, то есть система изолирована (замкнутая), из (3.12) выплывает, что

,

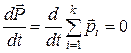или

(3.13)

Мы получили фундаментальный закон классической физики - закон сохранения импульса: в изолированной (замкнутой) системе суммарный импульс остается величиной постоянной. Для того, чтобы выполнялся закон сохранения импульса достаточно, чтобы система была замкнута.

Закон сохранения импульса является фундаментальным законом природы не знающим исключений.

В нерелятивистском случае можно ввести понятие центра масс (центра инерции) системы материальных точек, под которым понимают воображаемую точку, радиус-вектор которой , выражается через радиусы векторы материальных точек по формуле:

(3.14)

Найдем скорость центра масс в данной системе отсчета, взяв производную по времени от соотношения (3.14)

. (3.14)

Импульс системы равняется произведению массы системы на скорость ее центра инерции.

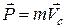. (3.15)

Понятие центра масс позволяет придать уравнению другую форму, которая часто оказывается более удобной. Для этого достаточно учесть, что масса системы есть величина постоянная. Тогда

(3.16)

где – сумма всех внешних сил, которые действуют на систему. Уравнение (3.16) – уравнение движения центра инерции системы. Теорема о движении центра масс гласит: центр масс движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на систему.

Если система замкнута, то . В этом случае уравнение (3.16) переходит в , из которого следует V=const. Центр масс замкнутой системы движется прямолинейно и равномерно.

Date: 2015-11-13; view: 331; Нарушение авторских прав