Связь потенциальной энергии с силой поля

Если известна потенциальная сила, действующая на тело, то пользуясь , можно найти потенциальную энергию тела. Пусть под действием силы тело переместилось на 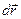вдоль некоторого направления S (см. рис.)

Т.к. работа сил потенциального поля равна убыли потенциальной энергии: , то

Скалярное произведение можно представить как 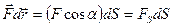, где - проекция силы на направление перемещения: . Подставим и получим

Откуда

Т.е. проекция силы на направление S равна взятой с обратным знаком производной от потенциальной энергии тела по координате S.

Теперь если взять последовательно в качестве направления перемещения направления вдоль осей декартовой системы координат, получим проекции силы:

Тогда сила

Градиентом скалярной функции называют вектор, проекциями которого являются частные производные по соответствующим координатам, и который можно представить как произведение оператора Гамильтона - набла на эту функцию. Дифференциальный оператор обладает формальными свойствами вектора.

Тогда

Получили, что сила поля равна с обратным знаком градиенту потенциальной энергии этого поля.

Date: 2015-11-13; view: 336; Нарушение авторских прав