Решение

Поток энергии, излучаемый Солнцем, определяется соотношением

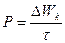- (1).

Изменение энергии Солнца в процессе излучения

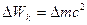- (2).

По условию - (3),

где m ₀ =1,989.1 0 ³⁰— начальная масса Солнца. Подставляя (2) в (1), с учетом (3),

получаем

,

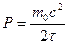откуда время, за которое масса Солнца уменьшится в 2 раза, равно

.

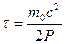Проверим единицы измерения определяемой величины.

.

Подставив числовые данные и вычисляя, получим

= .

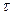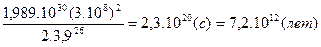Ответ 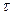=7,2.10 ¹² лет.

Задачи

1.1. Уравнение движения материальной точки вдоль оси имеет вид: х =А +Вt +Ct ³,

где А = 2 м, В = 1 м/с, С = -0,5 м/с ³ Найти координату х, скорость v и ускорение а точки в момент времени t = 2 с.

1.2. Тело вращается вокруг неподвижной оси по закону 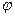= А + Вt + C t ², где А=10 рад, В= 20 рад/с, С=-2 рад/с ². Найти полное ускорение точки, находящейся на расстоянии

r = 0,1 м от оси вращения, для момента t = 4 с.

1.3.Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. За-кон движения автомобиля выражается уравнением: S=10 +10t - 0,5t ². Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения в момент времени t= 5 с.

I.4. Движение материальной точки задано уравнением х = А t + Bt ² , где А = 4 м/с,

В= -0,05 м/с ². Определить момент времени, в который скорость точки v= 0. Найти координату и ускорение в этот момент.

1.5. Точка движется по окружности радиусом 60 см с тангенциальным ускорением

10 см/с ². Чему равны нормальное и тангенциальное ускорения в конце третьей секунды после начала движения.Чему равен угол между векторами полного и нормального

ускорения в этот момент.

1.6. Материальная точка с массой m= 2 кг движется под действием некоторой силы согласно уравнению х = А + Вt + Сt ² + Dt ³, где C= 1 м/с ², D=-0,2 м/с³. Найти значение этой силы в момент времени t = 2 c. В какой момент времени сила равна нулю?

1.7. Маховик делал 4 оборота в секунду. При торможении он начал вращаться равно-замедленно и остановился через З с. Сколько оборотов сделал маховик до остановки?

1.8.Камень брошен с вышки со скоростью 29,4 м/с в горизонтальном направлении. Найти радиус кривизны траектории камня в точке, где он будет через 4 с после начала движения. Сопротивлением воздуха пренебречь.

1.9. Движения двух материальных точек выражаются уравнениями: х₁ = 20 + 2t – 4t ²,

х₂ = 2 + 2 t + 0,5t ^2. В какой момент времени скорости этих точек будут одинаковыми? Чему равны скорости и ускорения точек в этот момент?

1.10. Движение точки по прямой задано уравнением х =Аt + Bt², где А= 2 м/с, В=-0,5м/с². Определить скорость и ускорение движения точки в момент времени t = З с.

1.11. Движение точки по окружности радиуса R = 4 м задано уравнением S= А + Вt + Ct², где А = 10 м, В =-2 м/с, С = 1 м/с ². Найти тангенциальное, нормальное и полное ускоре-ния точки в момент времени t= 2 с.

.

1.12. Диск радиусом 20 см вращается согласно уравнению 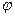= А +Bt+Ct ³, где А = З рад, В =-I рад/c, С = 0,1 рад/с ³. Определить тангенциальное, нормальное и полное ускорения точек на окружности диска для момента времени t = 10 с.

1.13. Линейная скорость точек на окружности вращающегося диска равна 6 м/с; точки, расположенные на 10 см ближе к оси, имеют линейную скорость 4 м/с. Сколько оборотов в секунду делает диск?

1.14. Маховик вращается по закону, выражающемуся уравнением 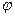= 0,5 t ². Найти угловую скорость и угловое ускорение маховика в момент времени t= 2 с. Найти танген-циальное, нормальное и полное ускорения в этот момент для точки, лежащей на маховике на расстоянии 0,8 м от оси вращения.

1.15. Тело брошено со скоростьюvо = 15 м/с под углом 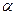= 30° к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) высоту h подъема тела; 2) дальность полета (по

горизонтали) s тела; 3) время t его движения.

1.16. Тело брошено со скоростью vо =20 м/с под углом 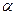= 30° к горизонту. Пренебрегая сопротивлением воздуха, определить для момента времени t = 1,5 с после начала движе-ния: 1) нормальное ускорение; 2) тангенциальное ускорение.

1.17. Зависимость пройденного телом пути от времени задается уравнением s =А - Вt +

Сt² +Dt ³ (А = б м, B=3 м/с, С = 2 м/с², D = 1 м/с ³). Определить для тела в интервале времени от t ₁= 1с до t ₂ = 4с: 1)среднюю скорость; 2) среднее ускорение.

1.18. Зависимость пройденного телом пути от времени задается уравнением s = А + Вt + Сt ² + Dt ³ (С =0,1 м/с², D = 0,03 м/с ³). Определить: 1) через какое время после начала движения ускорение тела будет равно а =2 м/с²; 2) среднее ускорение тела за этот проме-

жуток времени.

1.19. Тело движется равноускоренно с начальной скоростью v ₀. Определить ускорение тела, если за время t =2с оно прошло путь s = 16 м и его скорость v = 3v _0.

1.20. Кинематические уравнения движения двух материальных точек имеют вид х₁ = А ₁ + В₁t² + С₁ t ³ и x _{2 =} А ₂ t + В₂t ²+ С₂t ³ , где В₁= 4 м/с², С₁= -3 м/с³, B₂ =-2 м/с ², С ₂ = 1 м/c³. Определить момент времени, для которого ускорения этих точек будут равны.

1.21. Кинематические уравнения движения двух материальных точек имеют вид х₁ = А₁ +

B ₁ t+C ₁t ² x ₂=A ₂ +B₂t+C ₂t ², где В₁ = В ₂, С₁ = -2 м/с², С ₂= 1 м/с². Определить: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а ₁ и а₂ для этого момента.

1.22. Радиус-вектор материальной точки изменяется со временем по закону 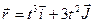, где 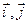— орты осей х и у. Определить для момента времени t = 1 с: 1) модуль скорости; 2) модуль ускорения.

1.23. Радиус-вектор материальной точки изменяется со временем по закону . Определить:1) скорость 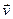; 2) ускорение 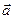; 3) модуль скорости в момент времени t= 2 с.

1.24. Диск радиусом R = 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 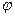= А + Вt +Сt ²- Dt ³ (В =

1 рад/с, С = 1 рад/с², D = 1 рад/с ³). Определить для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение а _t ; 2) нормальное ускорение а _n ; 3) полное ускорение а.

1.25. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 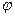= Аt ² (А = 0,5 рад/с ²). Определить к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения

1.26. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота ра-диуса диска от времени задается уравнением 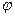= Аt ² (А = 0,1 рад/с ²). Определить пол-ное ускорение а точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки v= 0,4 м/с.

1.27. Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = At + Вt ² (А = 0,3 м/с², В = 0,1 м/с³). Определить момент времени, для которого вектор полного ускорения 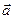образует с радиусом колеса угол 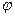= 4°.

1.28.Шайба, пущенная по поверхности льда с начальной скоростью v ₀₌ 20 м/с, останови-лась через t = 40 с. Найти коэффициент трения шайбы о лед.

1 29. Гиря массой 0,200 кг, привязанная к нити, опускается с ускорением 1 м/с ². Чему равно натяжение нити?

1.30. Шар массой m ₁₌ 10 кг сталкивается с шаром массой m ₂ = 4 кг Скорость первого шара v ₁₌ 4 м/с, второго – v ₂ = 12 м/с. Найти общую скорость u шаров после удара в двух случаях: когда малый шар нагоняет большой шар, движущийся в том же направлении; когда шары движутся навстречу друг другу. Удар считать прямым, неупругим.

1.31. Под действием постоянной силы F вагонетка прошла путь S= 5 м и приобрела ско-ростьv = 2 м/с. Определить работу А силы, если масса вагонетки m= 400 кг и коэффи-циент трения f=0,01.

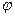1.32. Найти работу подъема груза по наклонной плоскости, если масса груза m= 100 кг, длина наклонной плоскости = 2 м, угол наклона = 30 ⁰, коэффициент трения f = 0,1 и груз движется с ускорением а = 1м/с².

1.33. Тело массой 1 кг, брошенное с вышки в горизонтальном направлении со скоростью v= 20 м/с, через 3 с упало на землю. Определить кинетическую энергию, которую имело тело в момент удара о землю.

1.34. Масса снаряда m ₁= 10 кг, масса ствола орудия m ₂ = 600 кг. При выстреле снаряд получает кинетическую энергию Т = 1,8 МДж. Какую кинетическую энергию получает ствол орудия вследствие отдачи?

1.35.Шайба, пущенная по поверхности льда с начальной скоростью v ₀₌ 20 м/с, останови-лась через t = 40 с. Найти коэффициент трения шайбы о лед.

1.36. Из орудия, укрепленного на железнодорожной платформе, произвели выстрел в направлении железнодорожного пути. Масса снаряда 40 кг, начальная скорость 500 м/с. Масса платформы с орудием 20.10 ³ кг. На какое расстояние откатится платформа, если коэффициент трения 0,002?

1.37. Шар массой m ₁₌ 10 кг сталкивается с шаром массой m ₂ = 4 кг Скорость первого шара v ₁₌ 4 м/с, второго – v ₂ = 12 м/с. Найти общую скорость u шаров после удара в двух

случаях: когда малый шар нагоняет большой шар, движущийся в том же направлении;

когда шары движутся навстречу друг другу.Удар считать прямым и неупругим.

1.38. Автомобиль массой m =1,8 т спускается при выключенном двигателе с постоянной скоростьюv =54 км/ч по уклону дороги (угол к горизонту 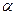=3 ⁰). Определить, какова должна быть мощность двигателя автомобиля, чтобы он смог подниматься на такой же подъем с той же скоростью.

1.39. Материальная точка массой m = 1кг двигалась под действием некоторой силы согласно уравнению s=А-Вt+Сt ²-Dt ³ (В= З м/с,С=5м/с², D=1м/с ³). Определить мощ-

ность N, затрачиваемую на движение точки в момент времени t = 1 с.

1.40. Поезд массой m = 600 т движется под гору с уклоном 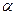=3 ⁰ и за время t = 1 мин развивает скорость v= 18 км/ч. Коэффициент трения f=0,01. Определить среднюю мощ-ность 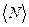локомотива.

1.41. Тело брошено вертикально вверх со скоростью v ₀=20 м/с. Пренебрегая сопротив-лением воздуха, определить, на какой высоте h кинетическая энергия тела будет равна

его потенциальной энергии.

1.42. Подвешенный на нити шарик массой m = 200г отклоняют на угол 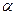= 45°. Опре-делить силу натяжения нити в момент прохождения шариком положения равновесия.

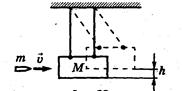1.43. Пуля массой m =15 г, летящая с горизонтальной ско-

ростью v = 0,5 км/с, попадает в баллистический маятник масс-

сой М = б кг (рис. 1) и застревает в нем. Определить высоту

h, на которую поднимется маятник, откачнувшись после удара.

Рис.1

1.44. Пуля масой m = 15 г, летящая горизонтально, попадает в баллистический маятник длиной =. 1 м и массой М = 1,5 кг и застревает в нем (рис.1). Маятник в результате этого отклонился на угол 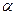= 30°. Определить скорость пули.

1.45. Пуля массой m = 15 г, летящая горизонтально со скоростью v = 200 м/с, попадает в баллистический маятник (рис.1) длиной 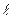= 1 м и массой М =.1,5 кг и застревает в нем. Определить угол отклонения 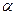маятника.

1.46. Тело массой m ₁ = 3 кг движется со скоростью v₁= 2 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, определить количество теп-лоты, выделившееся при ударе.

1.47. Два шара массами m ₁ = 9 кг и m ₂ = 12 кг подвешены на нитях длиной 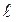= 1,5 м. Первоначально шары соприкасаются между собой, затем меньший шар отклонили на

угол = 30 ⁰ и отпустили. Считая удар неупругим, определите высоту h, на которую поднимутся оба шара после удара.

1.48. Два шара массами m ₁ = 3 кг и m ₂ = 2 кг подвешены на нитях длиной 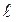= 1 м. Первоначально шары соприкасаются между собой, затем больший шар отклонили от положения равновесия на угол = 60° и отпустили. Считая удар упругим, определить скорость 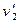второго шара после удара.

1.49. Два шара массами m ₁ = 200 г и m ₂₌. 400 г подвешены на нитях длиной 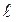=67,5 см. Первоначально шары соприкасаются между собой, затем первый шар отклонили от поло-жения равновесия на угол = 60° и отпустили. Считая удар упругим, определите, на ка-кую высоту h поднимется второй шар после удара.

1.50. Определить момент инерции тонкого однородного стержня длиной 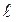= 50 см и массой m =360 г относительно оси, перпендикулярной стержню и проходящей через:

1) конец стержня; 2) точку, отстоящую от конца стержня на 1/6 его длины.

1.51. Шар и сплошной цилиндр одинаковой массы, изготовленные из одного и того же материала, катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.

1.52. Полная кинетическая энергия Т диска, катящегося по горизонтальной поверхности, равна 24 Дж. Определить кинетическую энергию Т ₁ поступательного и Т₂ вращательного движения диска.

1.53. Полый тонкостенный цилиндр массой m = 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену v₁=1,4 м/с, после удара 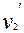=1 м/с. Определить выделившееся при ударе количество теплоты.

1.54. Шар радиусом R = 10 см и массой m = 5 кг вращается вокруг оси симметрии соглас-но уравнению 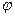= А + Вt ² + Сt ³ (В =2 рад/с², С =-0,5 рад/с³). Определить момент сил М для t = З с.

1.55. Вентилятор вращается с частотой n = 600 об/мин. После выключения он начал вра-щаться равнозамедленно и, сделав N = 50 оборотов, остановился. Работа А сил тормо-жения равна 31,4 Дж. Определить: 1) момент М сил торможения; 2) момент инерции J вентилятора.

1.56. Маховик в виде сплошного диска, момент инерции которого J = 150 кг м ², вращает-ся с частотой n = 240 об/мин. Через время t = 1 мин, как на маховик cтал действовать мо-мент сил торможения, он остановился. Определить: 1) момент М сил торможения; 2) чис-ло оборотов маховика от начала торможения до полной остановки.

1.57.К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная, касательная сила F= 100 Н. При вращении диска на него действует момент сил трения

М _тр = 2 Н м. Определить массу m диска, если известно, что его угловое ускорение ε постоянно и равно 16 рад/с ².

1.58. Частота вращения n ₀ маховика, момент инерции которого равен J=120 кг м², состав-ляет 240 об/мин. После прекращения действия на него вращающего момента маховик под действием сил трения в подшипниках остановился за время t = 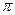мин. Считая трение в подшипниках постоянным, определить момент М сил трения.

1.59. Маховик в виде сплошного диска, момент инерции которого J = 1,5 кг.м², вращаясь при торможении равнозамедленно, за время t = 1 мин уменьшил частоту своего вращения с n ₀ = 240 об/мин до n ₁ = 120 об/мин. Определить: 1) угловое ускорение маховика; 2) мо-мент силы торможения; 3) работу торможения А.

1.60. Колесо радиусом R = 30 см и массой m = 3 кг скатывается без трения по наклонной плоскости длинно 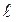= 5 м и углом наклона = 25°. Определить момент инерции колеса, если его скорость v в конце движения составляла 4,6 м/с.

1.61. Полый тонкостенный цилиндр катится вдоль горизонтального участка дороги со ско-ростью v = 1,5 м/с. Определить путь, который он пройдет в гору за счет кинетической энергии, если уклон горы равен 5 м на каждые 100 м пути.

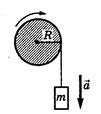
1.62. На однородный сплошной вал (рис.2) радиусом R=50 см

намотана легкая нить, к концу которой прикреплен груз мас-

сой m = 6,4 кг. Груз, разматывая нить, опускается с a = 2 м/с².

Определить: 1)момент инерции J вала;2) массу М вала.

Рис.2

1. 63. Маховик начинает вращаться из состояния покоя с постоянным угловым ускоре-нием ε = 0,4 рад/с². Определить кинетическую энергию маховика через время t ₂= 25 с после начала движения, если через t ₁ = 10 с после начала движения момент импульса L ₁ маховика составляет б0 кгм²/с.

1.64. Горизонтальная платформа массой m =25 кг и радиусом R= 0,8 м вращается с час-тотой n ₁ = 18 мин^-1. В центре стоит человек и держит в расставлеянных руках гири. Счи-тая платформу диском, определите частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от J₁ = 3,5кг.м ² до J ₂=1кг.м².

1.65. Человек массой m = 60 кг, стоящий на краю горизонтальной платформы массой М = 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n₁ = 10 мин^-1, переходит к ее центру. Считая платформу круглым однородным диском, а чело-века — точечной массой, определить, с какой частотой n ₂ будет тогда вращаться платфор-ма.

1.66. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

1.67. Человек массой m = 60 кг, стоящий на краю горизонтальной платформы радиусом

R = 1 м и массой M= 120 кг, вращающейся по инерции вокруг неподвижной вертикаль-ной оси с частотой n ₁=10 мин^-1, переходит к ее центру. Считая платформу круглым одно-родным диском, а человека — точечной массой, определить работу, совершаемую чело-веком при переходе от края платформы к ее центру.

1.68. Маховик делал 5 об/с. Под действием постоянного тормозящего момента, равного 1000 Нм, он остановился через 20 с. Определить момент инерции маховика.

1.69.Маховик в виде диска массой 50 кг и радиуса 0,2 м вращается, делая 10 оборотов в секунду. Определить кинетическую энергию маховика.

1.70. На барабан радиусом R=0,5 м намотан шнур, к концу которого привязан груз массой m ₁₌10 кг. Найти момент инерции барабана, если известно, что груз опускается с ускоре-нием а = 2,04 м/с².

1.71. Диск массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска.

1.72. Шар диаметром б см катится без скольжения по горизонтальной плоскости, делая 4 об/с. Масса шара 0,25 кг. Найти кинетическую энергию шара.

1.73. Медный шар радиуса R= 10 см вращается со скоростью соответствующей частоте

n = 2 об/с вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое?

I.74. Мальчик катит обруч по горизонтальной дороге со скоростью 7,2 км/ч. На какое расстояние может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен 10 м на каждые 100 м пути.

1.75. Найти кинетическую энергию велосипедиста, едущего со скоростью v = 9 км/ч. Мас-са велосипедиста вместе с велосипедом m= 78 кг, причем на массу колес приходится m₁ = З кг. Колеса велосипеда считать обручами.

1.76. Грузик, привязанный к нити, описывает в горизонтальной плоскости окружность радиуса 10 см, делая 1 оборот в секунду. Какой угол образует нить с вертикалью?

I.77. Найти линейные скорости движения центра масс шара и диска, скатывающихся без скольжения с наклонной плоскости. Высота наклонной плоскости h= 0,5 м, начальная скорость тел равна нулю.

1.78. Стержень длиной 0,6 м и массой 04 кг вращается с ускорением 10 рад/с ² около оси, проходящей через середину стержня перпендикулярно его длине. Найти вращающий момент.

1.79. Определить работу, которую необходимо затратить, чтобы сжать пружину на 15 см, если известно, что сила пропорциональна деформации и под действием силы 20 Н пружи-на сжимается на 1 см.

1.80. Определить относительное удлинение алюминиевого стержня, если при его растя-жении затрачена работа А = 6,9 Дж. Длина стержня 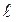= 1. м, площадь поперечного се-чения S = 1 мм², модуль Юнга для алюминия Е = 69 ГПа.

1.81. Мезон, входящий в состав космических лучей, движется со скоростью, составляю-щей 95% скорости света. Какой промежуток времени по часам земного наблюдателя соответствует одной секунде собственного времени мезона.

1.82. Мезоны космических лучей достигают поверхности Земли с самыми разными скоростями. Найти релятивистское сокращение размеров мезона, имеющего скорость, равную 95% скорости света.

1,83. Две ракеты летят в одном направлении со скоростями соответственно 0,9 и 0,6 с относительно лабораторной системы координат. Найти скорость первой ракеты отно-сительно наблюдателя, находящегося во второй ракете.

1.84. Ускоритель сообщил радиоактивному ядру скорость 0,4 с. В момент вылета из ускорителя ядро выбросило в направлении своего движения 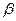— частицу со скоростью 0,75 с относительно ускорителя. Найти скорость этой частицы относительно ядра.

1.85. Какую скорость необходимо сообщить телу, чтобы его плотность возросла на 10%?

1.86. Какую долю скорости света должна составлять скорость частицы, чтобы ее кинети-ческая энергия была равна энергии покоя?

1.87. Вычислить импульс протона, если известно, что его кинетическая энергия равна

500 МэВ.

1.88. На сколько изменится масса 1 кг льда при плавлении? Удельная теплота плавления льда З,З.I0⁵ Дж/кг.

1.89.Какова кинетическая энергии протона, если его масса больше массы покоя на вели-чину, составляющую 5% от массы покоя?

1.90. Покажите, что события, происходящие однсвременно в различных точках в одной инерциальной, системе отсчета, не одновременны в другой инерциальной системе отсчета.

1.91. Пользуясь преобразованиями Лоренца, выведите релятивистский закон сложения скоростей при переходе от системы К к системе К^'.

1.92. Определить, во сколько раз увеличивается время жизни нестабильной частицы (по часам неподвижного наблюдателя), если она начинает двигаться со скоростью, равной

0,9 с.

I.93. Определить относительную скорость движения, при которой релятивистское сокра-щение линейных размеров тела составляет 10%.

1.94. Определите собственную длину стержня, если в лабораторной системе его скорость v = 0,бс, длина 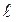=1,5 м и угол между стержнем и направлением его движения = 30°.

1.95. Воспользовавшись тем, что интервал является инвариантной величиной по отноше-нию к преобразованиям координат, определить расстояние, которое пролетел 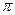-мезон с момента рождения до распада, если время его жизни в этой системе отсчета 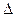t = 4,4 мкс, а собственное время жизни 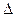t ₀= 2,2 мкс.

1.96. Определить скорость движения релятивистской частицы, если ее масса в два раза больше массы покоя.

1.97. Определить релятивистский импульс протона, если скорость его движения v =0,8с.

1.98. Определить скорость, при которой релятивистский импульс частицы превышает ее ньютоновский импульс в n=3 раза.

1.99. Полная энергия релятивистской частицы в 8 раз превышает ее энергию покоя. Опре-делите скорость этой частицы.

1.100. Кинетическая энергия частицы оказалась равной ее энергии покоя. Определить ско-рость частицы.

1.101. Определить релятивистский импульс р и кинетическую энергию Т протона, движу-щегося со скоростью v = 0,75с.

1.102. Определить кинетическую энергию электрона, если масса движущегося электрона втрое больше его массы покоя. Ответ выразить в электронвольтах.

1.103. Определить, какую ускоряющую разность потенциалов должен пройти протон, что-бы его скорость составила 90% скорости света.

1.104. Определить, какую ускоряющую разность потенциалов должен пройти электрон, чтобы его продольные размеры уменьшились в два раза.

1.105. Определить работу, которую необходимо совершить, чтобы увеличить скорость частицы с массой m от 0,5с до 0,7с.

1.106. Выведите в общем виде зависимость между релятивистским импульсом, кинети-ческой энергией релятивистской частицы и ее массой.

1.107. Определить релятивистский импульс электрона, кинетическая энергия которого

Т = 1 ГэВ.

1.108. Во сколько раз изменится площадь круга, если он будет двигаться со скоростью 200000 км/с в направлении одного из его радиусов.

.

1.109. Прямоугольный стеклянный брусок движется вдоль одного из своих ребер со ско-ростью 290000 км/с. Какова плотность этого бруска в состоянии движения, если таблич-ная плотность данного сорта стекла 2,45.10 ³ кг/м³?

1.110. Две частицы с одинаковыми скоростями v₁ = v₂ = 3/4с 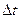движутся по одной прямой и попадают в мишень. Одна из частиц попала в мишень позже другой на время 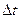= 10 ^-8с. Найти расстояние между частицами в полете в системе отсчета, связанной с ними.

ПРИЛОЖЕНИЯ

Единицы механических величин

Наименование величин	Единица
Определяющее уравнение	обозначение	Наименование и определение
Скорость		м/с	Метр в секунду равен скорости равномерного и прямолинейного движения, при котором точка за 1 с перемещается на расстояние 1 м
Ускорение		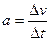м/с2	Метр в секунду в квадрате равен уско-рению прямолинейного ускоренного движения точки,при котором за 1 с ско-рость точки изменяется на 1 м/с.
Угловая скорость		Рад/с	Радиан в секунду равен угловой скорости равномерного вращающегося тела, все точки которого за 1 с поворачиваются на угол 1 рад.
Угловое ускорение		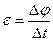Рад/с2	Радиан в секунду в квадрате равен угло-вому ускорению равноускоренно враща-ющегося тела,при котором оно за 1 с из-менит угловую скорость на 1 рад/с
Частота перио- дического процесса		Гц	Герц равен частоте периодического про-цесса,при которой за 1 с совершается 1 цикл процесса
Плотность		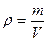кг/м3	Килограмм на кубический метр рамен плотности однородного вещества, маса которого при объеме 1 м3 равна 1 кг
Сила	F=ma	Н	Ньютон равен силе, которая массе 1кг сообщает ускорение 1 /с2 в направлении действия силы:1Н=1кг.м/с2.
Импульс	P=mv	кг.м/с	Килограмм-метр в секунду равен импульсу материальной точки массой 1 кг, движущейся со скоростью 1 м/с.
Давление	Р=	Па	Паскаль равен давлению,создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности пло-щадью 1 м2: 1 Па=1Н/м2
Работа єнергия	A=Fs	Дж	Джоуль равен работе, совершаемой силой 1 Н на пути 1 м: 1Дж=1 Н.м
Мощность	N=	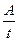Вт	Ватт равен мощности, при которой за время 1 с совершается работа 1 Дж: 1 Вт=1Дж/с
Момент инерции	J=mr2	кг.м2	Килограмм-метр в квадрате равен мо-менту инерции материальной точки масссой 1 кг, находящейся от оси на расстоянии 1 м.
Момент силы	M=F	Н.м	Ньютон-метр равен моменту силы, рав-ной 1Н, относительно точки располо-женной на расстоянии 1м от линии дей-ствия силы
Момент импульса	L=mvr	кг.м2./с	Килограмм-метр в квадрате на секунду равен моменту импульса материальной точки, движущейся по окружности ра-диусом 1м и имеющей импульс 1кг.м/с

Date: 2015-11-13; view: 2026; Нарушение авторских прав