Рабочая программа. Курса общей физики по разделу“механика”

курса общей физики по разделу“Механика”

1. Физические основы классической механики

Классическая механика — одно из оснований современной техники. Механическое движение. Кинематика. Тело отсчета, система отсчета. Материальная точка. Скорость и ускорение. Нормальное и тангенциальное ускорения.

Кинематика вращательного движения абсолютно твердого тела. Угловая скорость и угло-вое ускорение, их связь с линейными скоростями и ускорениями точек вращающегося те-ла.

Динамика. Задачи динамики. Первый закон Ньютона. Инерциальные и неинерциальные системы отсчета. Масса. Импульс. Сила. Фундаментальные взаимодействия. Второй закон Ньютона. Третий закон Ньютона.

Динамика вращательного движения тела вокруг неподвижной оси. Момент импульса. Момент инерции тела относительно оси. Момент силы. Уравнение динамики вращатель-ного движения твердого тела относительно неподвижной оси.

Механическая работа и энергия. Работа силы и ее выражение через криволинейный интеграл. Понятие о поле. Энергия как универсальная мера различных форм движения и взаимодействия. Механическая энергия. Кинетическая энергия механической системы и ее связь с работой внешних и внутренних сил, приложенных к системе. Кинетическая энергия вращающегося тела.

Потенциальные поля. Силы потенциальные (консервативные) и диссипативные. Потен-циальная энергия тела в гравитационном поле. Потенциальная энергия упругого взаимо-действия.

Законы сохранения — фундаментальные законы физики. Закон сохранения импульса. Закон сохранения момента импульса. Закон сохранения механической энергии. Общий закон сохранения энергии.

2. Элементы специальной теории относительности

Пространство и время. Пространство и время в классической механике. Преобразования Галилея. Принцип относительности Галилея. Постулаты специальной теории относитель-ности. Преобразования Лоренца. Относительность понятия одновременности событий. Относительность временных интервалов. Лоренцево сокращение длины. Релятивистский закон сложения скоростей. Интервал между событиями и его инвариантность по отноше-нию к выбору инерциальной системы отсчета как проявление и взаимосвязь пространства и времени.

Элементы релятивистской динамики. Импульс и масса в релятивистской динамике. Основной закон релятивистской динамики материальной точки. Взаимосвязь массы и энергии. Релятивистское выражение для кинетической энергии. Соотношение между пол-ной энергией и импульсом.

Основные законы и формулы

1.1. Элементы кинематики

Средняя и мгновенная скорости материальной точки

, ,

, v= ,

где - элементарное перемещение точки за промежуток времени 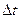; - радиус-вектор точки; - путь, пройденный точкой за промёжуток времени .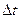

Среднее и мгновенное ускорения материальной точки

,

Полное ускорение при криволинейном движении

= ,

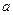где а_t = - тангенциальная составляющая ускорения;

а _n - нормальная составляющая ускорения (R-радиус кривизны траектории в данной точке).

Путь, скорость для равнопеременного движения

;

,

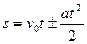где v₀ -начальная скорость.

Угловая скорость

.

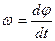Угловое ускорение

Угловая скорость для равномерного вращательного движения

,

где Т-период вращения; n = - частота вращения (N — число оборотов, совершаемых телом за время t).

Угол поворота и угловая скорость для равнопеременного вращательного движения

;

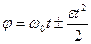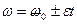
где ₀ - начальная угловая скорость.

Связь между линейными и угловыми величинами:

; v=R ; a_t=R ε; а_{n = ,}

где R- расстояние точки от оси вращения.

1.2. Динамика материальной точки и поступательного движения твердого тела

Импульс (количество движения) материальной точки

Второй закон Ньютона (основное уравнение динамики материальной точки)

=m = .

Это же уравнение в проекциях на касательную и нормаль к траектории точки

.

Сила трения скольжения

Fтр = f N,

гдеf - коэффициент трения скольжения; N- сила нормального давления.

Сила трения качения

Fтр = ,

где f_k - коэффициент трения качения; г - радиус катящегося тела.

Закон сохранения импульса для замкнутой системы

где n - число материальных точек (или тел), входящих в систему.

1.З. Работа и энергия

Работа, совершаемая постоянной силой,

,

где F_s - проекция силы на направление перемещения;

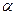- угол между направлениями силы и перемещения.

Работа, совершаемая переменной силой, на пути s

А= .

Средняя мощность за промежуток времени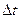

Мгновенная мощность

или .

Кинетическая энергия движущегося со скоростью v тела массой m

T= .

Связь между силой, действующей на тело в данной точке поля, и потенциальной энергией тела

или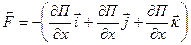

- единичные векторы координатных осей.

Потенциальная энергия тела, поднятого над поверхностью земли на высоту h,

П =mgh,

гдеg - ускорение свободного падения.

Сила упругости

F=-kx

где х - деформация; к- коэффициент упругости.

Потенциальная энергия упруго деформированного тела

.

Закон сохранения механической энергии (для консервативной системы)

Т + П = Е =.соnst.

Коэффициент восстановления

где и -соответственно нормальные составляющие относительной скорости тел после и до удара.

Скорости тел массами m₁и m₂ после их абсолютно упругого центрального удара

,

,

где v ₁ и v₂ - скорости этих тел до удара.

Скорость тел массами m ₁ и m ₂, движущихся соответственно со скоростями v ₁ и v₂, после абсолютно неупругого центрального удара

.

1.4.Механика твердого тела

Момент инерции материальной точки

,

где m-масса точки; r-расстояние до оси вращения.

Момент инерции системы (тела)

,

где r_{і -} расстояние материальной точки массой m _і до оси вращения; в случае непрерывного распределения масс

.

Моменты инерции тел правильной геометрической формы (тела считаются однородными; m масса тела):

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиусом R	Ось симметрии	mR2
Сплошной цилиндр или диск радиусом R	То же
Прямой тонкий cтержень длиной	Ось перпендикулярна cтержню и проходит через его середину
То же	Ось перпендикулярна и проходит через его конец
Шар радиусом R	Ось проходит через центр шара

Теорема Штейнера

_,

где J_с- момент инерции тела относительно оси, проходящей через центр масс; J — момент инерции относительно параллельной оси, отстоящей от первой на расстоянии а; m —мас-са тела.

Кинетическая энергия тела, вращающегося вокруг неподвижной осиz,

_,

где J_z — момент инерции тела относительно оси; -его угловая скорость.

Кинетическая энергия тела, катящегося по плоскости бёз скольжения,

T= ,

где m- масса тела; v_c — скорость центра масс тела; J_c — момент инерции тела относительно оси, проходящей через его центр масс; — угловая скорость тела.

Момент силы относительно неподвижной точки

,

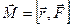где — радиус-вектор, проведенный из этой точки в точку приложения силы . Модуль момента силы

М=F ,

где — плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).

Работа при вращении тела

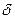А=М_z d ,

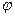где d 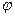— угол поворота тела; М_z — момент силы относительно оси z.

Момент импульса (момент количества движения) твердого тела относительно оси

вращения

,

где r_{і -} расстояние от оси z отдельной частицы тела; m_і v_і –импульс этой частицы; J_z –мо-

мент инерции тела относительно оси z; -его угловая скорость.

Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси

,

ε— угловое ускорение; J_z — момент инерции тела относительно оси z.

Закон сохранения момента импульса (момента количества движения) для замкнутой системы

.

Напряжение при упругой деформации тела

,

где F - растягивающая (сжимающая) сила; S—площадь поперечного сечения тела.

Относительное продольное растяжение (сжатие)

,

где — изменение длины тела при растяжении (сжатии)

—длина тела до деформации.

Относительное поперечное растяжение (сжатие)

где — изменение диаметра стержня при растяжении (сжатии);d— диаметр стержня.

Закон Гука для продольного растяжения (сжатия)

где Е-модуль Юнга.

Потенциальная энергия упруго растянутого (сжатого) тела

,

где V-объем тела.

1.5. Элементы специальной (частной) теории относительности

Преобразования Лоренца

x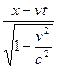^' = , у^'=у, z^'=z‚ ,

где предполагается, что система отсчета К^' движется со скоростью v в положительном направлении оси x системы отсчета К, причем оси х^' и х совпадают, а оси у^' и у, z^' и z, параллельны; с — скорость распространения света в вакууме.

Релятивистское замедление хода часов

^{' =}

Где 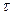-промежуток времени между двумя событиями, отсчитанный движущимися вместе с телом часами; 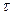^'- промежуток времени между теми же событиями, отсчитанный покоящимися часами.

Релятивистское (лоренцево) сокращение длины

,

l ₀— длина стержня, измеренная в системе отсчета, относительно которой стержень покоится (собственная длина); l — длина стержня, измеренная в системе отсчета относительно которой он движётся со скоростью v.

Релятивистский закон сложения скоростей

_{, , ,}

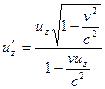где предполагается, что система отсчета К^' движется со скоростью v в положительном направлении оси х системы отсчета К, причем оси х^' и х совпадают, оси у^' и у,z^' и z параллельны.

Интервал S₁₂ между событиями (инвариантная величина)

где t₁₂ — промежуток времени между событиями 1 и 2;

l ₁₂— расстояние между точками, где произошли события.

Релятивистский импульс частицы

,

где m — масса частицы.

Основной закон релятивистской динамики

,

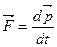где релятивистский импульс.

Полная и кинетическая энергия релятивистской частицы

; Т=Е-Е_0,

где Е ₀ — энергия покоя (m масса частицы; с — скорость распространения света в вакууме).

Связь между энергией и импульсом релятивистской частицы

Е² = m²с⁴ + р²с ^2, pc= .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Диск радиусом R = 5 см вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением = 2Аt + 5Вt ⁴

(А =2рад/с ², В = 1 рад/с ⁵). Определить для точек на ободе диска к концу первой секунды после начала движения: 1) полное ускорение; 2) число оборотов, сделанных диском.

Дано:R=5см=0,05м, В=5см=0,О5м, =2Аt+5Вt ⁴, А=2рад/с², В=1рад/с⁵, t = 1 с.

Определить: 1) а; 2) N.

Решение. Полное ускорение , где тангенциальная составляющая ускорения ( -угловое ускорение), а нормальная составляющая ускорения

.

По условию задачи следовательно,

,

,

откуда полное ускорение

.

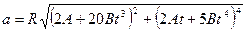Угол поворота диска (N —. число оборотов), но угловая скорость 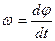следовательно,

.

. Тогда число оборотов, сделанных диском,

.

Проверим единицы измерения.

[а]= [м ] = , N-единиц измерения не имеет.

Подставив числовые данные, получим:

а = 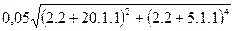= 4,22(м/с²),

N= 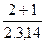=0,477 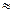0,5.

Ответ: 1) а = 4,22 м/с ² , 2) N 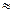0,5.

Задача 2. На барабан радиусом R = 20 см, момент инерции которого J = 0,1 кг м², намотан шнур к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h ₀ =1м. Через какое время t груз опустится до пола? Найти кинетическую энергию W _k, груза в момент удара о пол и силу натяжения нити Т.Трением пренебречь.

Дано: R=20 cм = 0,2м, J=0,1кгм ², m=0,5кг, h₀ =1м

Определить: 1) t; 2) W_{k ;} 3) Т.

Решение.

При опускании груза его потенциальная энергия переходит в кинетическую энергию поступательного движения и кинетическую энергию вращательного движения: - (1),

где 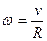, откуда 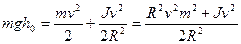или

; (2).

Движение равноускоренное, поэтому Рис.1

(3); Рис.1

. (4).

Выразим t из (4) и подставив в 2) получим:

;

Кинетическая энергия , подставив уравнение (2), получим

.

По второму закону Ньютона

mg -T= ma, откуда T= m(g- а).

Из (3): ,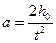

Тогда .

Проверим единицы измерения и проведем вычисления t, W_K и Т.

= ,

, .

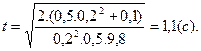
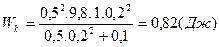Ответ: t=1,1с; W_k=0,82Дж; Т=4,1Н.

Задача 3. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня 1=1 м. Найти скорость v пули, если известно, что стержень с шаром отклонился от удара пули на угол а =10°.

Дано: М=1000 m, =1м, .

Определить v.

Date: 2015-11-13; view: 603; Нарушение авторских прав