Решение. Рассмотрим движение центра масс карандаша

Рассмотрим движение центра масс карандаша. В вертикальном положении он обладает потен-циальной энергией, которая при падении переходит в кинетическую энергию вращения (рис.7).

- (1).

Момент инерции карандаша относительно оси, проходящей через его конец, найдем по теореме Штёйнера:

- (2).

Подставив (2) в (1), получим

,откуда ;

= 14 рад/с. Поскольку = = , а линейная скорость v= R, то скорость конца карандаша v ₁ = =2,1м_./с. Скорость середины 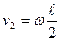=1,05 м/с.

Ответ: v₁=2,1м /с, v ₂=!,05м/с.

Задача10. Горизонтальная платформа (рис.8) массой m =100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n ₁ =10 об/мин. Человек массой m ₀ =60 кг стоит при этом на краю платформы. С какой частотой n ₂ начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека — точечной массой.

Дано: m=100 кг, n₁ =10 об/мин_, m ₀=60 кг.

Определить n _2.

Решение:

Система «человек - платформа» замкнута в проекции на ось у,

т. к. моменты сил М_mg =0 и M _m0g =0 в проекции на эту ось. Сле-

довательно, можно воспользоваться законом сохранения момента Рис.8

импульса. В проекции на ось у:

J₁ w ₁= J ₂ w ₂ - (1),

где J ₁- момент инерции платформы с человеком, стоящим на ёе краю, J ₂ - момент инерции платформы с человеком, стоящим в центре, w ₁ и w ₂ - угловые скорости платформы в обоих случаях. Здесь

- (2),

где R- радиус платформы. Подставляя (2) в (1) и учитывая, что , где n - частота вращения платформы, получим:

; .

Вычисляя, получим

Ответ n ₂ =22об/мин.

Задача11. Доказать, что при малых скоростях релятивистская формула кинетической энергии переходит в классическую.

Date: 2015-11-13; view: 419; Нарушение авторских прав