Основные формулы. 6.1.Кинематические уравнение гармонических колебаний материальной точки:

6.1.Кинематические уравнение гармонических колебаний материальной точки:

или

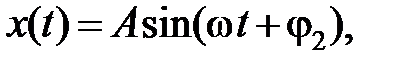
где x (t)– смещение колеблющейся точки от положения равновесия;

А – амплитуда колебания;

– круговая или циклическая частота;

– начальные фазы колебаний.

6.2. Связь циклической частоты с частотой колебаний и периодом Т колебаний:

6.3. Скорость и ускорение материальной точки, совершающей гармонические колебания:

6.4. Сила, действующая на материальную точку:

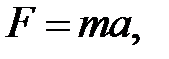
где m – масса точки.

6.5. Полная энергия материальной точки m, совершающей гармонические колебания:

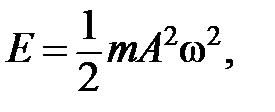
где А – амплитуда колебаний;

– циклическая частота;

k –жёсткость пружины.

6.6. Сложение гармонических колебаний одного направления и одинаковой частоты:

а) уравнение результирующего гармонического колебания:

б) амплитуда результирующего колебания:

в) начальная фаза результирующего колебания:

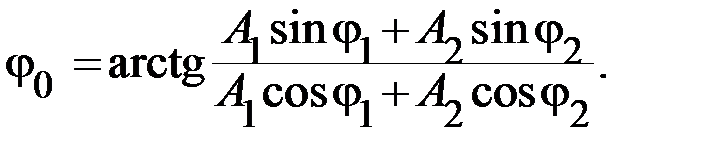
6.7. Траектория точки, участвующей в двух взаимноперпендикулярных колебаниях

;

а) если разность фаз

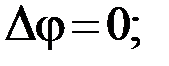
б) 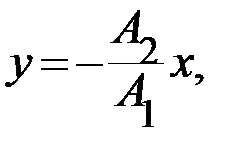если разность фаз

в) если разность фаз

6.8. Период колебания маятников:

пружинного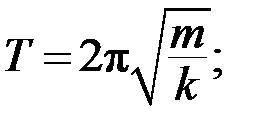

математического

физического

где m – масса маятника;

k – жесткость пружины;

l – длина маятника;

J – момент инерции маятника;

g – ускорение свободного падения;

L – расстояние от точки подвеса до центра масс.

6.9. Уравнение затухающих колебаний:

,

где – зависимость амплитуды колебаний от времени 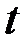; 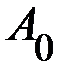–начальная амплитуда; – основание натурального логарифма; –коэффициент затухания; – коэффициент сопростивления.

Частота затухающих колебаний:

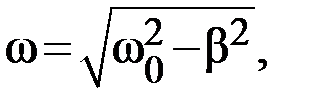
где 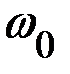– частота свободных колебаний.

Логарифмический декремент затухания:

где и – амплитуды двух последовательных колебаний отстоящих по времени друг от друга на период .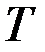

Амплитуда вынужденных колебаний:

где – амплитудное значение внешней периодической силы.

Резонансная частота и резонансная амплитуда:

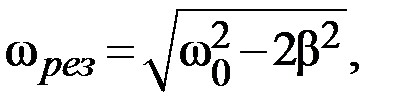
6.10. Уравнение плоской волны, распространяющейся в направлении оси OX:

или

где – смещение любой из точек среды с координатой х в момент времени t; – скорость волнового процесса в среде; k – волновое число; 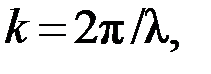– длина волны.

6.11. Длина волны:

где Т – период;

– частота волны.

6.12. Разность фаз колебаний двух точек среды:

где – длина волны;

– расстояние между точками среды (разность хода).

6.13. Фазовая скорость продольных волн в упругой среде:

где – модуль Юнга;

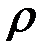– плотность вещества;

или

где 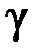– показатель адиабаты ( – отношение удельных теплоёмкостей при постоянном давлении и постоянном объёме).

– молярная газовая постоянная;

– термодинамическая температура;

– молярная масса;

– давление газа.

6.14. Аккустический эффект Допплера:

где 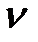– частота звука, воспринимаемого движущимся прибором (или ухом);

– скорость звука в среде;

– скорость прибора относительно среды;

– скорость источника звука относительно среды;

– частота звука, испускаемого источником.

Date: 2015-11-13; view: 717; Нарушение авторских прав