Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Умножение матрицы на число
|
|
Результатом умножения матрицы на число является матрица,каждый элемент которой умножен на это число.
Пример. Даны матрицы:
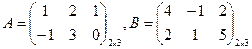
Вычислить матрицу 
Умножение матриц
Результатом умножения матриц будет матрица, каждый элемент которой является результатом перемножения соответствующей строки первой матрицы на соответствующий столбец второй матрицы.
Перемножаются только такие две матрицы, у которых число столбцов равно числу строк второй матрицы.
Пример:
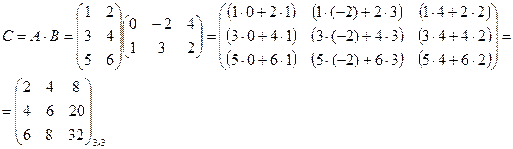
Замечание. Если посчитаем
Как видно, 
Системы линейных уравнений.
Рассмотрим систему двух линейных уравнений с двумя неизвестными в общем виде:
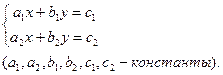(1)
Решение методом исключения переменных.
1 шаг (исключаем y). Помножим 1-ое уравнение на 
, второе уравнение – на 
и из первого вычтем второе:
(2)
2 шаг (исключаем х). По аналогичной схеме:
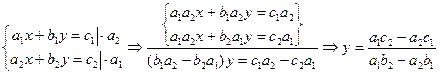(3)
Выражения для х, у справедливы, если знаменатель 
В этом случае имеем единственное решение системы (1).
В противном случае система либо не имеет решений, либо имеет их бесконечное множество.
Примеры. Решить системы уравнений.
По формулам (2), (3) находим:
Знаменатель не равен 0 и найденное решение единственно.
Знаменатель и числитель в выражении 
по формулам(2),(3)равны 0.
В этом случае система имеет бесконечное множество решений. Как видим, второе уравнение получается из первого умножением на 2.
В соответствии с формулами (2), (3):
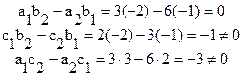
В этом случае система не имеет решений (несовместна). Действительно, домножим первое уравнение на 2:
Пришли к противоречию.
Решение системы (1) можно представить в другом виде. Рассмотрим основную матрицу коэффициентов системы:
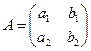(4)
Определителем матрицы А называетсячисло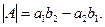 
Как видим, его значение совпадает со знаменателем выражений (2), (3).
Введем вспомогательные матрицы:
(5)
Здесь столбец коэффициентов при х (соответственно – у) заменяется на столбец свободных членов.
Определители матриц:
;
(6)
соответствуют числителям в выражениях (2), (3).
Во введенных обозначениях решение системы (1) перепишется: 
Такой ход решения системы (1) соответствует методу (или правилу) Крамера и естественно обобщается на трехмерный (и более мерный) случай.
Система линейных алгебраических уравнений в трехмерном случае:
(7)
Основная матрица коэффициентов системы имеет вид:
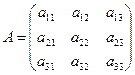
Ее определитель будем вычислять в соответствии со схемой:
(8)
(+) (–)
Со знаком «+» берутся произведения элементов, соединенных по левой схеме, со знаком «‑» - по правой.
Вспомогательные матрицы определяются как и в 2-мерном случае:
Их определители считаются в соответствии со схемой (8).
Date: 2015-12-10; view: 453; Нарушение авторских прав