
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Линейное векторное пространство. Базис. Размерность
|
|
Рассмотрим непустое множество V элементов – «векторов», зададим на нём две линейные операции – сложение векторов и умножение вектора на действительное число, тогда, если эти линейные операции обладают ниже перечисленными свойствами, то это непустое множество V называется линейным векторным пространством. Выпишем эти свойства:
1º.  ; 2°.
; 2°. 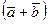 +
+  ;
;
3º.  ; 4°.
; 4°. 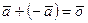 ;
;
5º. a 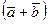 =a
=a  +a
+a  ; 6°(a1+a2)
; 6°(a1+a2)  =a1
=a1  +a2
+a2  ;
;
7º. a1·(a2  )=(a1·a2)
)=(a1·a2)  ; 8°.
; 8°.  =a
=a  , (т.е. a=1), где a1, a2, a3
, (т.е. a=1), где a1, a2, a3  R.
R.
Линейной комбинацией системы векторов  ,
,  , …,
, …,  называется вектор
называется вектор 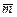 = a1
= a1  +a2
+a2  +…+ak
+…+ak  , а числа ai – ее коэффициенты.
, а числа ai – ее коэффициенты.
Рассмотрим линейную комбинацию, являющуюся нуль вектором:
a1  +a2
+a2  +…+an
+…+an  =
=  (*).
(*).
Заметим, что равенство (*) имеет место всегда для нулевых коэффициентов (ai – все нули), но может возникнуть та ситуация, когда оно выполняется и для ненулевой системы коэффициентов, тогда в этом случае говорят, что данная система векторов – линейно зависима, в противном случае – линейно независима (т.е. когда равенство выполняется только для нулевой системы коэффициентов).
Остановимся на примерах:
1°.  ;
;  , причем
, причем  ||
||  ,
,  . Тогда
. Тогда  =a·
=a·  a·
a·  ,
,  = –a, т.е. система коэффициентов – нетривиальная, значит, по определению эта пара векторов есть пример линейно зависимой системы.
= –a, т.е. система коэффициентов – нетривиальная, значит, по определению эта пара векторов есть пример линейно зависимой системы.
2°.  , где
, где  – компланарны и
– компланарны и 

 . Тогда
. Тогда  =a·
=a·  +b·
+b·  a·
a·  +b·
+b·  –
–  =a,
=a,  =b,
=b,  , следовательно, имеем пример линейно зависимой системы.
, следовательно, имеем пример линейно зависимой системы.
3°.  , где
, где  . Тогда, образовав равенство a·
. Тогда, образовав равенство a· 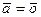 , получим, что оно возможно только для случая, когда a= 0 (т.е. только для тривиальной системы коэффициентов), значит, один ненулевой вектор образует линейно независимую систему.
, получим, что оно возможно только для случая, когда a= 0 (т.е. только для тривиальной системы коэффициентов), значит, один ненулевой вектор образует линейно независимую систему.
4°.  , где
, где 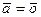 , тогда равенство a·
, тогда равенство a· 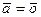 возможно для любых a, т.е. и для a
возможно для любых a, т.е. и для a  0,значит, это пример линейно зависимой системы.
0,значит, это пример линейно зависимой системы.
5°. Неколлинеарные векторы образуют линейно независимую систему векторов (методом от противного было бы получено, что они коллинеарны).
6°. Некомпланарная тройка векторов образует линейно независимую систему (по аналогии – метод от противного привел бы нас к тому, что они компланарны).
Из определения линейно зависимой системы векторов можно получить признак (критерий) линейной зависимости: система векторов линейно зависима тогда и только тогда, когда один из векторов этой системы является линейной комбинацией остальных.
Базисом векторного пространства называется упорядоченная система линейно независимых векторов, через которую можно разложить любой вектор пространства, причем, коэффициенты разложения вектора  пространства V будут называться координатами этого вектора в базисе.
пространства V будут называться координатами этого вектора в базисе.
Размерностью векторного пространства называется число векторов базиса.
Так, если рассмотреть базис  в V 3, то
в V 3, то  или
или  (X; Y; z).
(X; Y; z).
Формулы перехода от одного базиса к другому
Рассмотрим задачу перехода от одного базиса к другому, а именно: найдем связь координат произвольного вектора  в разных базисах. Для простоты рассмотрим пространство V 2 и пусть исходный базис в нем
в разных базисах. Для простоты рассмотрим пространство V 2 и пусть исходный базис в нем  . Другой базис {
. Другой базис {  } задан в исходном таким образом:
} задан в исходном таким образом:
 =(
=( ;
;  ),
),  =(
=( ;
;  ).
).
Вектор 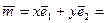 (x; y) – старые его координаты;
(x; y) – старые его координаты;
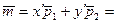 (
( ;
;  ) – новые его координаты.
) – новые его координаты.

 . Но
. Но 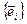 – базис, значит, последнее равенство имеет место только при нулевых коэффициентах (согласно определению линейно независимой системы). Итак, получим:
– базис, значит, последнее равенство имеет место только при нулевых коэффициентах (согласно определению линейно независимой системы). Итак, получим:  – формулы перехода от одного базиса к другому.
– формулы перехода от одного базиса к другому.
Матрица Т перехода от одного базиса к другому имеет вид: Т =  . Заметим, что первый столбец (а 11; а 21) этой матрицы – координаты первого вектора нового базиса, а второй столбец (а 12; а 22) – координаты второго вектора нового базиса в исходном базисе
. Заметим, что первый столбец (а 11; а 21) этой матрицы – координаты первого вектора нового базиса, а второй столбец (а 12; а 22) – координаты второго вектора нового базиса в исходном базисе 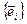 . В матричном виде эти формулы запишутся: Х = ТX ¢, где Х =
. В матричном виде эти формулы запишутся: Х = ТX ¢, где Х =  , X ¢=
, X ¢=  .
.
Аналогичные формулы можно получить и для n-мерного пространства.
Date: 2015-12-10; view: 431; Нарушение авторских прав