Решение матричных уравнений

Рассмотрим матричное уравнение вида АХ = В, где А и В – данные матрицы, а Х – искомая матрица. Пользуясь обратной матрицей, можно найти матрицу Х. Для этого умножим обе части уравнения слева на А^-1, тогда получим А ^-1(АХ) = = А ^-1 В. По ассоциативному закону А ^-1(АХ)= (А ^-1 А) Х = ЕХ = Х, т.е. решение запишется так: Х = А ^-1∙ В. Если же имеем уравнение ХА = В, то решение его будет иметь вид: Х = ВА ^-1. Рассмотрим уравнения, в которых матрица А – невырожденная.

Пример:

Решить уравнение ∙ Х = .

А = ; В = ; Х = .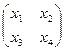

1-й шаг. А ^-1 –? 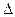А =–2; А ^*= , А ^-1= .

2-й шаг. Проверка: А ^-1∙ А = ∙ = =Е.

3-й шаг. А ^-1∙ В = ∙ = = 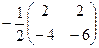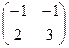, Х = .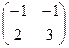

4-й шаг. Проверка: ∙ = = .

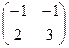Ответ: Х = .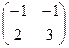

Замечание. Линейную систему можно рассматривать как матричное уравнение, в котором матрица В – одностолбцовая матрица, а её элементы – свободные члены линейной системы; матрица Х является также одностолбцовой, а её элементы – неизвестные х ₁, х ₂, х ₃,…, х_n.

Так, линейная система: может быть записана в виде: АХ = В, где А = , В = , Х = 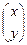. Поэтому решением этой системы является матрица Х = А ^-1∙ В.

Предлагаем решить эту систему самостоятельно, используя А ^-1 (Ответ: Х = ).

Date: 2015-12-10; view: 832; Нарушение авторских прав