Задачи на прямую, решаемые методом координат

Раздел 1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ И ЛИНЕЙНАЯ АЛГЕБРА

Декартова система координат. Прямая на плоскости

Если на плоскости выбраны две взаимно перпендикулярные прямые Ох и Оу с указанными на них положительными направлениями и разметкой в соответствии с заданной единицей масштаба, то говорят, что задана декартова прямоугольная система координат.

Историческая справка: Область математики – аналитическая геометрия – связывается с именем выдающегося французского математика 17 века Рене Декарта (1595-1650). В 1637г. опубликована его книга «Геометрия» в качестве приложения к «Рассуждению о методе», где изложены основы аналитической геометрии. Как отмечается исследователями (Стройк Д.Я., 1990): «Вместе с многими другими великими мыслителями 17 века, Декарт искал общий метод мышления, который бы позволял быстрее делать изобретения и выявлять истину в науке… Он последовательно применил хорошо развитую алгебру начала 17 века к геометрическому анализу древних и таким образом в огромной мере расширил область ее применимости…».

При этом каждой точке плоскости М соответствует единственная пара действительных чисел (х, у) – ее координат, причем соответствие взаимно-однозначное (т.е. верно и обратное).

Задачи на прямую, решаемые методом координат

1. Расстояние между парой точек А (х ₁, у ₁) и В (х ₂, у ₂).

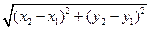
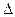= (следует из теоремы Пифагора для прямоугольного треугольника АВС).

2. Деление отрезка (АВ) в заданном отношении.

Пусть 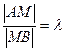( - заданное число).

Тогда если провести МЕ || AC || OX, то из подобия треугольников () следует: = ;

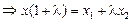
аналогично .

В частности, если М – середина отрезка АВ, то есть если :

; .

3. Уравнение прямой линии.

а) «С угловым коэффициентом»:

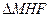Продолжим отрезок АВ до пересечения с осью ОY (в точке Н (0, b)) и с осью ОХ (в точке Р). Пусть HF || O X, тогда и из tg = = .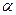

Откуда y – b = kx (k = tg 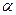- «угловой коэффициент прямой»).

Окончательно: y = kx + b.

б) «Проходящей через заданную точку (А) в заданном направлении (задан угол )».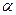

Из : tg = tg = k =

.

в) «Проходящей через две заданные точки (А и В)».

Из подобия треугольников :

.

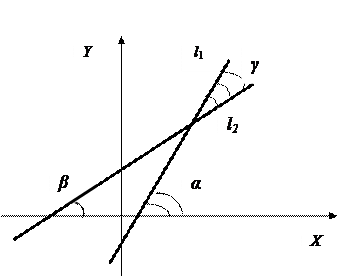
4. Угол между прямыми

Пусть заданы прямые: l ₁: y= k ₁ x + b ₁ (k ₁ =tg 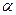); l ₂: y= k ₂ x + b ₂ (k ₂ =tg ).

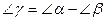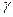Тогда , tg 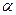= tg 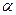( - )=(tg -tg )/(1+tg tg ).

Или через угловые коэффициенты tg 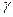=(k ₁ – k ₂ )/(1+ k ₁ k ₂ ).

5. Условия параллельности и перпендикулярности прямых.

l ₁ // l ₂ tg (k ₁ – k ₂)/(1+ k ₁ k ₂) k ₁ = k ₂.

l ₁ l ₂ 1+ k ₁ k ₂=0 k ₂= -1/ k ₁.

Задача: Известны координаты вершин треугольника 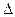АВС: А (5, 0), В (17, -9), С (21, 13). Требуется определить:

Длину стороны АВ,

Уравнения сторон АВ, АС,

Угол ВАС (в градусах и радианах),

Уравнение высоты CD (проведенной из вершины С) и ее длину,

Уравнение медианы АЕ (Е – середина ВС),

Уравнение прямой, проходящей через точку С, параллельно стороне АВ.

Решение: -1) |AB| = = = 15.

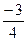2) Уравнение АВ: (k_AB= ). Уравнение АС: 16 y = 13(x – 5) y = (k_AC = ).

3) tg A = (k_AC – k_AB)/(1+ k_AC k_AB) = .

Откуда 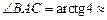76⁰.

4) .

Уравнение CD: y – 13 = 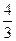(x – 21) = 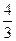x – 28 y = 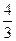x – 15.

Координаты точки D найдем из системы:

D:

.

Из системы находим y = -3. Окончательно: D (9, -3).

|CD | = =

5) Координаты точки Е:

x _E = ; y _E = E (19, 2).

Уравнение АЕ: 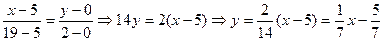(k_AE = ).

6) Пусть l – искомая прямая, тогда: k _l = k_AB = .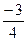

Уравнение l: y – 13 = -

Окончательно: y = - .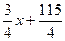

Date: 2015-12-10; view: 480; Нарушение авторских прав